题目内容
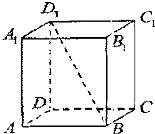
若四棱柱ABCD-A1B1C1D1的底边长为2，高为4，则异面直线BD1与AD所成角的正切值是
| 5 |
| 5 |
分析：由AD∥BC，知∠D1BC就是异面直线BD1与AD所成的角，由此能求出异面直线BD1与AD所成角的正切值．
解答：
解：∵AD∥BC，∴∠D1BC就是异面直线BD1与AD所成的角，
连接D1C，∵正四棱柱ABCD-A1B1C1D1的底边长为2，高为4，
∴BC=2，D1C=
=2
，BC⊥D1C，
∴异面直线BD1与AD所成角的正切值tan∠D1BC=
=
=
．
故答案为：
．
解：∵AD∥BC，∴∠D1BC就是异面直线BD1与AD所成的角，连接D1C，∵正四棱柱ABCD-A1B1C1D1的底边长为2，高为4，
∴BC=2，D1C=
| 4+16 |
| 5 |
∴异面直线BD1与AD所成角的正切值tan∠D1BC=
| D1C |
| BC |
2
| ||
| 2 |
| 5 |
故答案为：
| 5 |
点评：本题考查异面直线所成角的正切值的求法，解题时要认真审题，仔细解答，是基础题．
练习册系列答案
相关题目
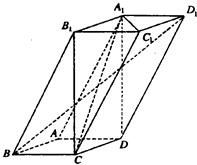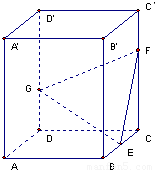
如图，四棱柱ABCD-A1B1C1D1中，A1D⊥平面ABCD，底面ABCD是边长为1的正方形，侧棱AA1=2．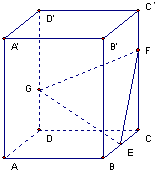
如图，正四棱柱ABCD-A′B′C′D′中，底面边长为2，侧棱长为3，E为BC的中点，FG分别为CC′、DD′上的点，且CF=2GD=2．求：
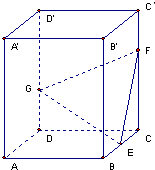如图，正四棱柱ABCD-A′B′C′D′中，底面边长为2，侧棱长为3，E为BC的中点，FG分别为CC′、DD′上的点，且CF=2GD=2．求：