题目内容
 如图,角α的顶点为原点O,始边为y轴的非负半轴、终边经过点P(-3,-4).角β的顶点在原点O,始边为x轴的非负半轴,终边OQ落在第二象限,且tanβ=-2,则cos∠POQ的值为( )
如图,角α的顶点为原点O,始边为y轴的非负半轴、终边经过点P(-3,-4).角β的顶点在原点O,始边为x轴的非负半轴,终边OQ落在第二象限,且tanβ=-2,则cos∠POQ的值为( )A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|
分析:由题意可求得cos(
+α)=-
,从而可求得sinα的值;利用∠POQ=(
+α)-β,利用两角和的余弦公式,可求得cos∠POQ=cos(
+α-β);
| π |
| 2 |
| 3 |
| 5 |
| π |
| 2 |
| π |
| 2 |
解答:解:依题意,角
+α的顶点在直角坐标原点,始边在y轴的正半轴、终边经过点P(-3,-4),
∴|OP|=5
∴cos (
+α)=-
,
∴sinα=
,即角α 的正弦值为
.
cos∠POQ=cos(
+α-β)
=cos(
+α)cosβ-sin(
+α)sinβ
又cos(
+α)=-
,sin(
+α)=-
∵tanβ=-2,β在第二象限,
∴sinβ=
,cosβ=-
,
∴cos∠POQ=(-
)×(-
)+(-
)×
=-
,
故选:A.
| π |
| 2 |
∴|OP|=5
∴cos (
| π |
| 2 |
| 3 |
| 5 |
∴sinα=
| 3 |
| 5 |
| 3 |
| 5 |
cos∠POQ=cos(
| π |
| 2 |
=cos(
| π |
| 2 |
| π |
| 2 |
又cos(
| π |
| 2 |
| 3 |
| 5 |
| π |
| 2 |
| 4 |
| 5 |
∵tanβ=-2,β在第二象限,
∴sinβ=
| 2 | ||
|
| 1 | ||
|
∴cos∠POQ=(-
| 3 |
| 5 |
| 1 | ||
|
| 4 |
| 5 |
| 2 | ||
|
| ||
| 5 |
故选:A.
点评:本题考查两角和与差的正弦函数,着重考察诱导公式及的作用及任意角的三角函数的定义,突出三角函数的综合应用,属于中档题.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
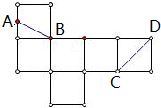 一个正方体的展开图如图所示,B,C,D为原正方体的顶点,A为原正方体一条棱的中点.在原来的正方体中,CD与AB所成角的余弦值为( )
一个正方体的展开图如图所示,B,C,D为原正方体的顶点,A为原正方体一条棱的中点.在原来的正方体中,CD与AB所成角的余弦值为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
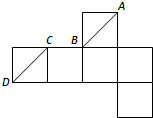 一个正方体的展开图如图所示,A、B、C、D为原正方体的顶点,则在原来的正方体中( )
一个正方体的展开图如图所示,A、B、C、D为原正方体的顶点,则在原来的正方体中( ) 一个正方体的展开图如图所示,A、B、C、D为原正方体的顶点,则在原来的正方体中( )
一个正方体的展开图如图所示,A、B、C、D为原正方体的顶点,则在原来的正方体中( )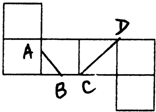 一个正方体的展开图如图示,C、D为原正方体的顶点,AB为原正方体的棱的中点,在原正方体中,CD与AB所成角的余弦值为( )
一个正方体的展开图如图示,C、D为原正方体的顶点,AB为原正方体的棱的中点,在原正方体中,CD与AB所成角的余弦值为( )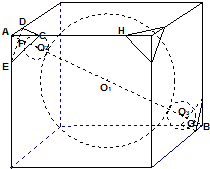 如图,一个棱长为a的立方体内有1个大球和8个小球,大球与立方体的六个面都相切,每个小球与大球外切且与共顶点的三个面也相切,现在把立方体的每个角都截去一个三棱锥,截面都为正三角形并与小球相切,变成一个新的立体图形,则原立方体的每条棱还剩余( )
如图,一个棱长为a的立方体内有1个大球和8个小球,大球与立方体的六个面都相切,每个小球与大球外切且与共顶点的三个面也相切,现在把立方体的每个角都截去一个三棱锥,截面都为正三角形并与小球相切,变成一个新的立体图形,则原立方体的每条棱还剩余( )