题目内容
17.函数y=x2(0≤x≤3)的最大值、最小值分别是( )| A. | 9和-1 | B. | 9和1 | C. | 9和0 | D. | 1和0 |
分析 根据二次函数的性质求出函数的单调性,从而求出函数的最大值和最小值即可.
解答 解:函数y=x2在[0,3]递增,
f(x)的最大值是9最小值是0,
故选:C.
点评 本题考查了二次函数的性质,考查函数的单调性问题,是一道基础题.

练习册系列答案
相关题目
7.已知椭圆和双曲线有共同的焦点F1,F2,P是它们的一个交点,且∠F1PF2=$\frac{π}{3}$,记椭圆和双曲线的离心率分别为e1,e2,则当e1e2取最小值时,e1,e2分别为( )
| A. | $\frac{1}{2}$,$\frac{\sqrt{5}}{2}$ | B. | $\frac{\sqrt{3}}{3}$,$\frac{\sqrt{6}}{2}$ | C. | $\frac{\sqrt{2}}{2}$,$\frac{\sqrt{6}}{2}$ | D. | $\frac{\sqrt{2}}{4}$,$\sqrt{3}$ |
8.某交警大队对辖区A路段在连续10天内的n天,对过往车辆驾驶员进行血液酒精浓度检查,查得驾驶员酒驾率f(n)如表;
可用线性回归模型拟合f(n)与n的关系.
(1)建立f(n)关于n的回归方程;
(2)该交警大队将在2016年12月11日至20日和21日至30日对A路段过往车辆驾驶员进行血液酒精浓度检查,分别检查n1,n2天,其中n1,n2都是从8,9,10中随机选择一个,用回归方程结果求两阶段查得的驾驶员酒驾率都不超过0.03的概率.
附注:
参考数据:$\sum_{n=5}^9{nf(n)=1.51}$,$\sum_{n=5}^9{{n^2}=255}$,$\overline{f(n)}$=0.046,回归方程$\widehat{f(n)}$=$\widehat{b}$n+$\widehat{a}$中斜率和截距最小乘估计公式分别为:$\widehatb=\frac{{\sum_{n=5}^9{nf(n)-5\overline{nf(n)}}}}{{\sum_{n=5}^9{{n^2}-5{{\overline n}^2}}}}$,$\widehata=\overline{f(n)}$-$\widehatb\overline n$.
| n | 5 | 6 | 7 | 8 | 9 |
| f(n) | 0.06 | 0.06 | 0.05 | 0.04 | 0.02 |
(1)建立f(n)关于n的回归方程;
(2)该交警大队将在2016年12月11日至20日和21日至30日对A路段过往车辆驾驶员进行血液酒精浓度检查,分别检查n1,n2天,其中n1,n2都是从8,9,10中随机选择一个,用回归方程结果求两阶段查得的驾驶员酒驾率都不超过0.03的概率.
附注:
参考数据:$\sum_{n=5}^9{nf(n)=1.51}$,$\sum_{n=5}^9{{n^2}=255}$,$\overline{f(n)}$=0.046,回归方程$\widehat{f(n)}$=$\widehat{b}$n+$\widehat{a}$中斜率和截距最小乘估计公式分别为:$\widehatb=\frac{{\sum_{n=5}^9{nf(n)-5\overline{nf(n)}}}}{{\sum_{n=5}^9{{n^2}-5{{\overline n}^2}}}}$,$\widehata=\overline{f(n)}$-$\widehatb\overline n$.
6.对任意非零实数a、b,若a?b的运算原理如图所示,则(log28)?($\frac{1}{2}$)2=( ) 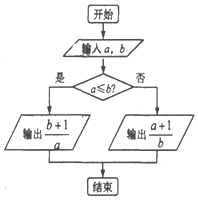

| A. | 16 | B. | 15 | C. | 14 | D. | 13 |
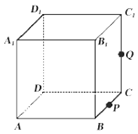 如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.
如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.