题目内容
13.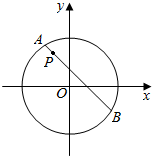 如图,圆O:x2+y2=8内有-点P(-1,2),AB为过P且倾斜角为135°的弦.
如图,圆O:x2+y2=8内有-点P(-1,2),AB为过P且倾斜角为135°的弦.(1)求AB的长;
(2)若圆C与圆O内切又与弦AB切于点P,求圆C的方程.
分析 (1)依题意直线AB的斜率为-1,直线AB的方程,根据圆心0(0,0)到直线AB的距离,由弦长公式求得AB的长.
(2)设圆C的圆心为(a,a+3),则$\sqrt{{a}^{2}+(a+3)^{2}}$=2$\sqrt{2}$-$\sqrt{(a+1)^{2}+(a+3-2)^{2}}$,求出a,即可求圆C的方程.
解答 解:(1)依题意直线AB的斜率为-1,直线AB的方程为:y-2=-(x+1),
圆心0(0,0)到直线AB的距离为d=$\frac{\sqrt{2}}{2}$,则|AB|=2$\sqrt{8-\frac{1}{2}}$=$\sqrt{30}$,∴AB的长为$\sqrt{30}$.
(2)过P与直线AB垂直的直线方程为y-2=x+1,即y=x+3,
设圆C的圆心为(a,a+3),则$\sqrt{{a}^{2}+(a+3)^{2}}$=2$\sqrt{2}$-$\sqrt{(a+1)^{2}+(a+3-2)^{2}}$,
∴a=-$\frac{3}{2}$,∴圆心为(-$\frac{3}{2}$,$\frac{3}{2}$),半径为$\frac{3}{2}$$\sqrt{2}$,
∴圆C的方程为(x+$\frac{3}{2}$)2+(y-$\frac{3}{2}$)2=$\frac{9}{2}$.
点评 本题考查用点斜式求直线方程,点到直线的距离公式,弦长公式的应用,考查圆的方程,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
3.过平面区域$\left\{\begin{array}{l}{x-y+2≥0}\\{y+a≥0}\\{x+y+2≤0}\end{array}\right.$,若z=x+2y的最小值为-8,则实数a=( )
| A. | -6 | B. | -5 | C. | -4 | D. | 2 |
2.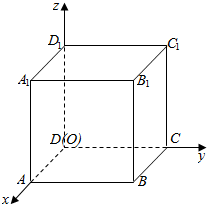 如图所示,以正方体ABCD-A1B1C1D1的顶点D为坐标原点O,如图建立空间直角坐标系,则与$\overrightarrow{{A}_{1}C}$共线的向量的坐标可以是( )
如图所示,以正方体ABCD-A1B1C1D1的顶点D为坐标原点O,如图建立空间直角坐标系,则与$\overrightarrow{{A}_{1}C}$共线的向量的坐标可以是( )
 如图所示,以正方体ABCD-A1B1C1D1的顶点D为坐标原点O,如图建立空间直角坐标系,则与$\overrightarrow{{A}_{1}C}$共线的向量的坐标可以是( )
如图所示,以正方体ABCD-A1B1C1D1的顶点D为坐标原点O,如图建立空间直角坐标系,则与$\overrightarrow{{A}_{1}C}$共线的向量的坐标可以是( )| A. | (1,$\sqrt{2}$,$\sqrt{2}$) | B. | (1,1,$\sqrt{2}$) | C. | ($\sqrt{2}$,-$\sqrt{2}$,$\sqrt{2}$) | D. | ($\sqrt{2}$,$\sqrt{2}$,1) |