题目内容
已知函数: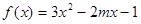 ,
,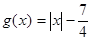 .
.
⑴解不等式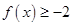 ;
;
⑵若对任意的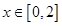 ,
,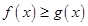 ,求
,求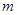 的取值范围.
的取值范围.
【答案】
(1) ①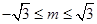 时,不等式的解为R; ②
时,不等式的解为R; ②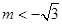 或
或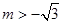 时,
时,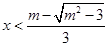 或
或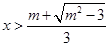 ;(2)
;(2)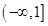 .
.
【解析】
试题分析:(1)含参数的二次不等式的解法要考虑判别式的值.(2)函数恒成立的问题,利用分离变量及基本不等式求最值的思想.
试题解析:⑴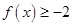 可化为
可化为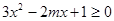 ,
,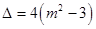 ,
,
①当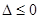 时,即
时,即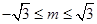 时,不等式的解为R;
时,不等式的解为R;
②当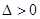 时,即
时,即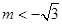 或
或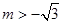 时,
时,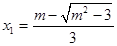 ,
,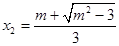 ,
,
不等式的解为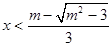 或
或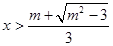 ;
;
(2)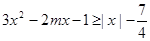 ,对任意的
,对任意的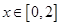 恒成立,
恒成立,
当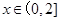 时,
时,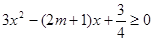 ,即
,即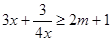 在
在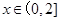 时恒成立;
时恒成立;
因为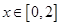 ,当
,当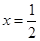 时等号成立.所以
时等号成立.所以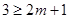 ,即
,即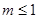 ;
;
当x=0显然成立.综上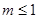 .
.
考点:1.含参数的不等式的解法.2.函数恒成立问题.3.基本不等式求最值问题.

练习册系列答案
相关题目
 .
. .
. 的解集为
的解集为 ,求实数
,求实数 的值;
的值; 使
使 成立,求实数
成立,求实数 的取值范围.
的取值范围. ,若不等式
,若不等式 的解集是空集,则( )
的解集是空集,则( ) B.
B. C.
C. D.
D.
 [来源:学#科#网]
[来源:学#科#网] ;⑵若
;⑵若 对于
对于 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。