题目内容
已知函数 .
.(1)解不等式f(x)>0;
(2)当x∈[1,4]时,求f(x)的值域.
【答案】分析:(1)先根据对数的运算性质对解析式化简,再令log2x=t代入f(x)>0,进而转化为关于t的二次不等式,求出t的范围再求对应的x的范围;
(2)由x∈[1,4]求出t∈[0,2],代入后进行配方,利用二次函数的性质求出f(x)的最值即可.
解答:解:(1)f(x)=
=(log2x-2)•(log2x+1)…(2分)
令log2x=t,∴f(x)=g(t)=(t-2)•(t+1),
由f(x)>0,可得(t-2)(t+1)>0,∴t>2或t<-1,…(4分)
∴log2x>2 或log2x<-1,∴x>4或 .…(6分)
.…(6分)
∴不等式的解集是 .…(7分)
.…(7分)
(2)∵x∈[1,4],∴t∈[0,2],…(8分)
∴ ,…(9分)
,…(9分)
∴ ,…(11分)
,…(11分)
fmax(x)=g(2)=0,…(13分)
∴f(x)的值域是 .…(14分)
.…(14分)
点评:本题考查了对数的运算性质,对数函数和二次函数性质的应用,以及换元法求函数的值域问题.
(2)由x∈[1,4]求出t∈[0,2],代入后进行配方,利用二次函数的性质求出f(x)的最值即可.
解答:解:(1)f(x)=

=(log2x-2)•(log2x+1)…(2分)
令log2x=t,∴f(x)=g(t)=(t-2)•(t+1),
由f(x)>0,可得(t-2)(t+1)>0,∴t>2或t<-1,…(4分)
∴log2x>2 或log2x<-1,∴x>4或
 .…(6分)
.…(6分)∴不等式的解集是
 .…(7分)
.…(7分)(2)∵x∈[1,4],∴t∈[0,2],…(8分)
∴
 ,…(9分)
,…(9分)∴
 ,…(11分)
,…(11分) fmax(x)=g(2)=0,…(13分)
∴f(x)的值域是
 .…(14分)
.…(14分)点评:本题考查了对数的运算性质,对数函数和二次函数性质的应用,以及换元法求函数的值域问题.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
已知函数f(x)的图象是不间断的,有如下的x,f(x)对应值:
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| f(x) | 136.136 | 15.552 | -3.92 | 10.88 | -52.488 | -232.064 | 11.238 |
由表可知函数f(x)存在实数解的区间有________个.
 ,
,
 为奇函数,求
为奇函数,求 的值。
的值。 ,有唯一实数解,求
,有唯一实数解,求 ,则是否存在实数
,则是否存在实数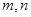 (
( ),使得函数
),使得函数 的定义域和值域都为
的定义域和值域都为 。若存在,求出
。若存在,求出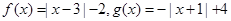 。
。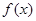 得值不大于1,求
得值不大于1,求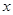 得取值范围;
得取值范围;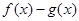
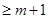 的解集为R,求
的解集为R,求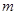 的取值范围。
的取值范围。