题目内容

20．几何体三视图如图所示，其中俯视图为边长为1的等边三角形，则此几何体的体积为$\frac{{\sqrt{3}}}{4}$．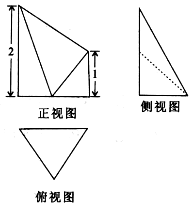

分析 几何体为四棱锥，棱锥的高为俯视图三角形的高，底面为直角梯形．

解答 解：由三视图可知，几何体为四棱锥，棱锥的高为俯视图中等边三角形的高$\frac{\sqrt{3}}{2}$，棱锥的底面为直角梯形，梯形面积为$\frac{1}{2}$（1+2）×1=$\frac{3}{2}$．
∴V=$\frac{1}{3}×\frac{3}{2}×\frac{\sqrt{3}}{2}$=$\frac{{\sqrt{3}}}{4}$．
故答案为$\frac{{\sqrt{3}}}{4}$．

点评 本题考查了棱锥的结构特征，三视图和体积计算，弄清三视图中的数据意义是关键．

练习册系列答案
相关题目
10．如图甲是某市有关部门根据当地干部的月收入情况调查后画出的样本频率分布直方图．已知图甲中从左到右第一组的频数为4000，在样本中记月收入在[1000，1500]，[1500，2000]，[2000，2500]，[2500，3000]，[3000，3500]，[3500，4000]的人数依次为A1，A2，…A6．图乙是统计图甲中月工资收入在一定范围内的人数的程序框图，则样本的容量n=10000，图乙输出的S=6000，（用数字作答）
11．（1）已知cos（15°+α）=$\frac{15}{17}$，α∈（0°，90°），求sin（15°-α） 的值．
（2）已知cosα=$\frac{1}{7}$，cos（α-β）=$\frac{13}{14}$，且0＜β＜α＜$\frac{π}{2}$，求β的值．
8．函数$y={log_2}（2sinx-1）+\sqrt{1-2cosx}$的定义域为[2kπ+$\frac{π}{3}$，2kπ+$\frac{5π}{6}$），（k∈z）．
15．已知角α终边经过点$（4sinθ，-3sinθ）θ∈（{π，\frac{3π}{2}}）$，求sinα，cosα，tanα．
5．定义运算a*b为执行如图所示的程序框图输出的S值，则${100^{（\frac{1}{2}lg9-lg2）}}*（{log_9}8•{log_4}\root{3}{3}）$的值为（　　）
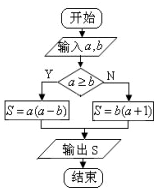
A．$\frac{13}{16}$B．$\frac{9}{2}$C．4D．6
12．${∫}_{0}^{π}$（cosx+2）dx等于（　　）
A．2πB．0C．π+2D．1
7．设数列{an}满足：${a_1}+\frac{a_2}{2}+\frac{a_3}{2^2}+…+\frac{{{a_{n+1}}}}{2^n}=2n+2$（n∈N*），且a2=4．
（1）求数列{an}的通项公式；
（2）设${b_n}={log_{\sqrt{2}}}{a_n}$，求数列{anbn}的前n项和Sn．
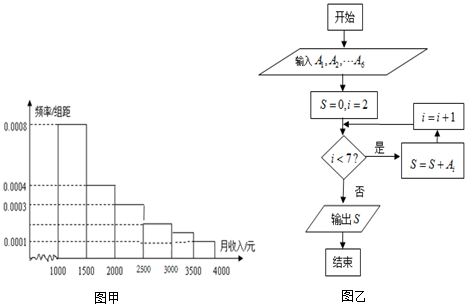
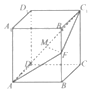8．已知四棱柱ABCD-A1B1C1D1中，AA1⊥平面ABCD，且四边形ABCD为菱形，F为棱BB1的中点，N为线段AC1的中点．
（1）求证：直线MF∥平面ABCD；
（2）求证：平面AFC1⊥平面ACC1A1．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网