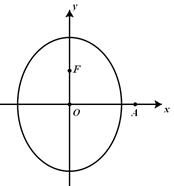
题目内容
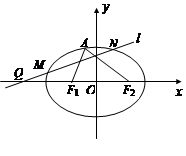
如图,已知椭圆C: 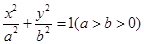 的左、右焦点分别为
的左、右焦点分别为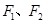 ,离心率为
,离心率为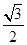 ,点A是椭圆上任一点,
,点A是椭圆上任一点,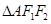 的周长为
的周长为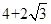 .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点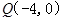 任作一动直线l交椭圆C于
任作一动直线l交椭圆C于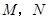 两点,记
两点,记 ,若在线段
,若在线段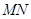 上取一点R,使得
上取一点R,使得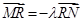 ,则当直线l转动时,点R在某一定直线上运动,求该定直线的方程.
,则当直线l转动时,点R在某一定直线上运动,求该定直线的方程.
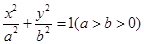 的左、右焦点分别为
的左、右焦点分别为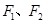 ,离心率为
,离心率为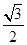 ,点A是椭圆上任一点,
,点A是椭圆上任一点,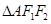 的周长为
的周长为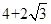 .
.(Ⅰ)求椭圆C的方程;
(Ⅱ)过点
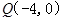 任作一动直线l交椭圆C于
任作一动直线l交椭圆C于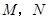 两点,记
两点,记 ,若在线段
,若在线段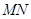 上取一点R,使得
上取一点R,使得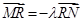 ,则当直线l转动时,点R在某一定直线上运动,求该定直线的方程.
,则当直线l转动时,点R在某一定直线上运动,求该定直线的方程.
(Ⅰ) ;(Ⅱ)
;(Ⅱ) .
.
 ;(Ⅱ)
;(Ⅱ) .
.试题分析:(Ⅰ)利用三角形
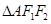 的周长为
的周长为 及离心率可求解;(Ⅱ)利用
及离心率可求解;(Ⅱ)利用 寻找
寻找 的坐标与实数
的坐标与实数 之间的关系,再利用
之间的关系,再利用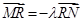 关系找到点R的坐标为(
关系找到点R的坐标为( )与
)与 之间的关系,化简求解.
之间的关系,化简求解.试题解析:(Ⅰ)∵
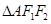 的周长为
的周长为 ,
,∴
 即
即 . (1分)
. (1分)又
 解得
解得 (3分)
(3分)∴椭圆C的方程为
 (4分)
(4分)(Ⅱ)由题意知,直线l的斜率必存在,
设其方程为

由

得
 (6分)
(6分)则
 (7分)
(7分)由
 ,得
,得
∴
 ∴
∴ . (8分)
. (8分)设点R的坐标为(
 ),由
),由 ,
,得

∴

解得
 (10分)
(10分)而


∴
 (13分)
(13分)故点R在定直线
 上. (14分)
上. (14分)
练习册系列答案
相关题目
 是它的两个顶点,直线
是它的两个顶点,直线 与直线
与直线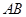 相交于点D,与椭圆相交于
相交于点D,与椭圆相交于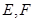 两点.
两点.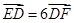 ,求
,求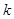 的值;
的值;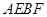 面积的最大值.
面积的最大值.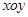 中,已知
中,已知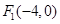 ,
,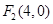 ,
,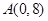 ,直线
,直线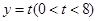 与线段
与线段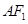 、
、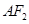 分别交于点
分别交于点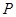 、
、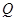 .
.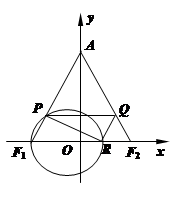
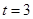 时,求以
时,求以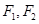 为焦点,且过
为焦点,且过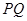 中点的椭圆的标准方程;
中点的椭圆的标准方程;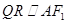 交
交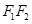 于点
于点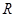 ,记
,记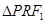 的外接圆为圆
的外接圆为圆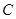 .
.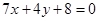 上;
上;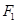 的一个定点?若过,求出该点的坐标;若不过,请说明理由.
的一个定点?若过,求出该点的坐标;若不过,请说明理由. 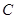 的对称中心为坐标原点,上焦点为
的对称中心为坐标原点,上焦点为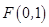 ,离心率
,离心率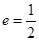 .
.
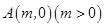 为
为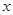 轴上的动点,过点
轴上的动点,过点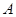 作直线
作直线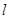 与直线
与直线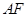 垂直,试探究直线
垂直,试探究直线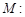
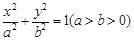 的四个顶点恰好是一边长为2,一内角为
的四个顶点恰好是一边长为2,一内角为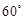 的菱形的四个顶点.
的菱形的四个顶点. 的方程;
的方程; 与椭圆
与椭圆 ,
, 两点,且线段
两点,且线段 的垂直平分线经过点
的垂直平分线经过点 ,求
,求 (
( 为原点)面积的最大值.
为原点)面积的最大值.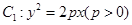 的焦点
的焦点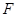 以及椭圆
以及椭圆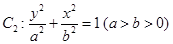 的上、下焦点及左、右顶点均在圆
的上、下焦点及左、右顶点均在圆 上.
上. 和椭圆
和椭圆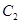 的标准方程;
的标准方程;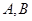 两不同点,交
两不同点,交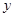 轴于点
轴于点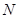 ,已知
,已知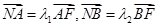 ,则
,则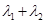
 是双曲线
是双曲线 的两个顶点,点
的两个顶点,点 是双曲线上异于
是双曲线上异于 (
( 为坐标原点)交椭圆
为坐标原点)交椭圆 于点
于点 ,如果设直线
,如果设直线 的斜率分别为
的斜率分别为 ,且
,且 ,假设
,假设 ,则
,则 的值为( )
的值为( )
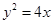 的焦点为F2,点F1与F2关于坐标原点对称,直线m垂直于x轴,垂足为T,与抛物线交于不同的两点P、Q且
的焦点为F2,点F1与F2关于坐标原点对称,直线m垂直于x轴,垂足为T,与抛物线交于不同的两点P、Q且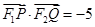 .
.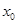 ;
;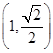 .
.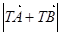 的取值范围.
的取值范围. 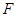 是椭圆
是椭圆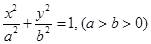 的左焦点,直线
的左焦点,直线 方程为
方程为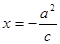 ,直线
,直线 轴交于
轴交于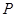 点,
点,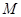 、
、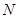 分别为椭圆的左右顶点,已知
分别为椭圆的左右顶点,已知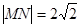 ,且
,且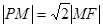 .
.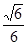 的直线交椭圆于
的直线交椭圆于 、
、 两点,求三角形
两点,求三角形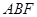 面积.
面积.