题目内容
(本小题满分12分)
已知双曲线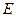 :
: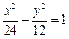 的
的 左焦点为
左焦点为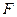 ,左准线
,左准线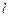 与
与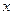 轴的交点是圆
轴的交点是圆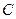 的圆心,圆
的圆心,圆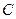 恰好经过坐标原点
恰好经过坐标原点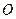 ,设
,设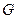 是圆
是圆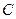
 上任意一点.
上任意一点.
(Ⅰ)求圆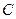 的方程;
的方程;
(Ⅱ)若直线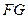 与直线
与直线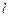 交于点
交于点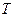 ,且
,且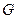 为线段
为线段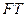 的中点,求直线
的中点,求直线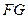 被圆
被圆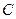 所截得的弦长;
所截得的弦长;
(Ⅲ)在平面上是否存在定点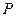 ,使得对圆
,使得对圆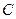 上任意的点
上任意的点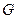 有
有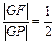 ?若存在,求出点
?若存在,求出点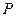 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
已知双曲线
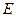 :
: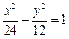 的
的 左焦点为
左焦点为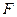 ,左准线
,左准线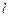 与
与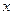 轴的交点是圆
轴的交点是圆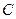 的圆心,圆
的圆心,圆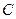 恰好经过坐标原点
恰好经过坐标原点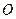 ,设
,设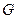 是圆
是圆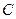
 上任意一点.
上任意一点.(Ⅰ)求圆
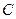 的方程;
的方程;(Ⅱ)若直线
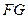 与直线
与直线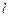 交于点
交于点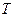 ,且
,且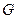 为线段
为线段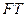 的中点,求直线
的中点,求直线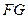 被圆
被圆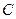 所截得的弦长;
所截得的弦长;(Ⅲ)在平面上是否存在定点
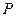 ,使得对圆
,使得对圆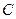 上任意的点
上任意的点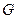 有
有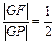 ?若存在,求出点
?若存在,求出点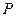 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.解:(Ⅰ)由双曲线E: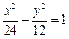 ,得
,得 :
:
 ,
, ,
, . …2分
. …2分
又圆C过 原点,所以圆C的方程为
原点,所以圆C的方程为 . …………………………3分
. …………………………3分
(Ⅱ)由题意,设 ,代入
,代入 ,得
,得 ,……………4分
,……………4分
所以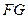 的斜率为
的斜率为 ,
,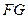 的方程为
的方程为 . ………………5分
. ………………5分
所以 到
到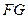 的距离为
的距离为 ,
,
直线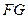 被圆C截得的弦长为
被圆C截得的弦长为 .
.
故直线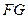 被圆C截得弦长为7. ……………………………………………………7分
被圆C截得弦长为7. ……………………………………………………7分
(Ⅲ)设 ,
, ,则由
,则由 ,得
,得 ,
,
整理得 .①……………………9分学
.①……………………9分学
又 在圆C
在圆C 上,所以
上,所以 .②
.②
②代入①,得 . ………………………10分
. ………………………10分
又由 为圆C 上任意一点可知,
为圆C 上任意一点可知, ,解得
,解得 .
.
所以在平面上存在一点P,其坐标为 . …………………………12分
. …………………………12分
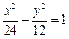 ,得
,得 :
:
 ,
, ,
, . …2分
. …2分又圆C过
 原点,所以圆C的方程为
原点,所以圆C的方程为 . …………………………3分
. …………………………3分(Ⅱ)由题意,设
 ,代入
,代入 ,得
,得 ,……………4分
,……………4分所以
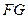 的斜率为
的斜率为 ,
,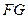 的方程为
的方程为 . ………………5分
. ………………5分所以
 到
到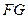 的距离为
的距离为 ,
,直线
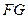 被圆C截得的弦长为
被圆C截得的弦长为 .
.故直线
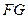 被圆C截得弦长为7. ……………………………………………………7分
被圆C截得弦长为7. ……………………………………………………7分(Ⅲ)设
 ,
, ,则由
,则由 ,得
,得 ,
,整理得
 .①……………………9分学
.①……………………9分学又
 在圆C
在圆C 上,所以
上,所以 .②
.②②代入①,得
 . ………………………10分
. ………………………10分又由
 为圆C 上任意一点可知,
为圆C 上任意一点可知, ,解得
,解得 .
.所以在平面上存在一点P,其坐标为
 . …………………………12分
. …………………………12分略

练习册系列答案
相关题目
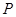 是双曲线
是双曲线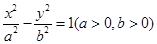 与圆
与圆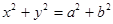 在第一象限的交点,其中
在第一象限的交点,其中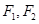 分别是双曲线的左、右焦点,且
分别是双曲线的左、右焦点,且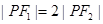 ,则双曲线的离心率为( )
,则双曲线的离心率为( )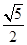
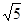
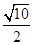
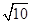
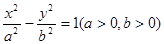 的离心率为
的离心率为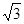 ,且它的一条准线与抛物线
,且它的一条准线与抛物线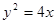 的准线重合,则此双曲线的方程为 ( )
的准线重合,则此双曲线的方程为 ( )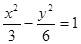
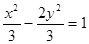
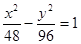

 ,其中正数a、b的等差中项是
,其中正数a、b的等差中项是 ,一个等比中项是
,一个等比中项是 ,且
,且 则双曲线的离心率为
则双曲线的离心率为 



 上一点,双曲线的一条渐近线方程为
上一点,双曲线的一条渐近线方程为 ,
, 分别是双曲线的左右焦点,若
分别是双曲线的左右焦点,若 ,则
,则 等于
等于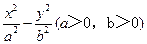 的一条渐近线的斜率为
的一条渐近线的斜率为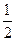 ,则该双曲线的离心率是
,则该双曲线的离心率是 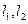 ,经
,经 过右焦点F垂直
过右焦点F垂直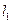 的直线分别交
的直线分别交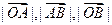 成等差数列,且
成等差数列,且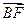 与
与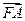 同向,则双曲线的离心率 .
同向,则双曲线的离心率 .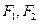 为双
为双 曲线C:
曲线C: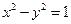 的左右焦点,点P在C上,
的左右焦点,点P在C上,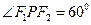 ,则P到x轴的距离为
,则P到x轴的距离为  ( )
( )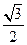
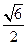
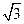
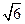
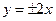 ,且过点
,且过点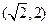 ,则此双曲线的标准方程为 .
,则此双曲线的标准方程为 .