题目内容
设点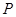 是双曲线
是双曲线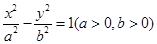 与圆
与圆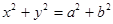 在第一象限的交点,其中
在第一象限的交点,其中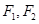 分别是双曲线的左、右焦点,且
分别是双曲线的左、右焦点,且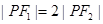 ,则双曲线的离心率为( )
,则双曲线的离心率为( )
 是双曲线
是双曲线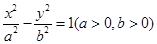 与圆
与圆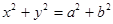 在第一象限的交点,其中
在第一象限的交点,其中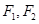 分别是双曲线的左、右焦点,且
分别是双曲线的左、右焦点,且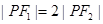 ,则双曲线的离心率为( )
,则双曲线的离心率为( )A.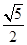 | B.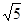 | C.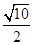 | D.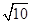 |
B
解:∵点P是双曲线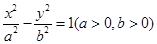 与圆x2+y2=a2+b2在第一象限的交点
与圆x2+y2=a2+b2在第一象限的交点
∴点P到原点的距离|PO|= =c,∠F1PF2=90°,
=c,∠F1PF2=90°,
∵|PF1|=2|PF2|,
∴|PF1|-|PF2|=|PF2|=2a,
∴|PF1|=4a,|PF2|=2a,
∴16a2+4a2=4c2,
∴5a2=c2,
∴e= =
=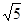 故答案为B
故答案为B
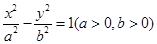 与圆x2+y2=a2+b2在第一象限的交点
与圆x2+y2=a2+b2在第一象限的交点∴点P到原点的距离|PO|=
 =c,∠F1PF2=90°,
=c,∠F1PF2=90°,∵|PF1|=2|PF2|,
∴|PF1|-|PF2|=|PF2|=2a,
∴|PF1|=4a,|PF2|=2a,
∴16a2+4a2=4c2,
∴5a2=c2,
∴e=
 =
=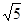 故答案为B
故答案为B
练习册系列答案
相关题目
 的一个焦点到一条渐近线的距离等于焦距的
的一个焦点到一条渐近线的距离等于焦距的 ,则该双曲线的离心率为 ( )
,则该双曲线的离心率为 ( )



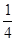
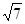 B、8, 6,
B、8, 6, 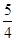 D、4, 3,
D、4, 3,  :
: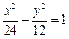 的
的 左焦点为
左焦点为 ,左准线
,左准线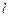 与
与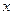 轴的交点是圆
轴的交点是圆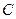 的圆心,圆
的圆心,圆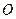 ,设
,设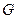 是圆
是圆 上任意一点.
上任意一点.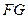 与直线
与直线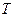 ,且
,且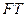 的中点,求直线
的中点,求直线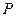 ,使得对圆
,使得对圆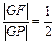 ?若存在,求出点
?若存在,求出点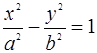 的一个焦点为
的一个焦点为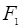 ,顶点为
,顶点为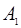 ,
,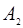 ,P是双曲线上任意一点,则分别以线段
,P是双曲线上任意一点,则分别以线段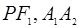 为直径的两圆一定( )
为直径的两圆一定( )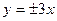 ,它的一个焦点是
,它的一个焦点是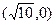 ,则该双
,则该双 的左、右焦点分别为
的左、右焦点分别为 为双曲线右支上—点,PF2与圆
为双曲线右支上—点,PF2与圆 切于点G,且G为
切于点G,且G为 的中点,则该双曲线的离心率e=__________
的中点,则该双曲线的离心率e=__________ -
- =1(a>0,b>0)的右焦点为F,右准线l与两条渐近线交于P、Q两点,如果△PQF是直角三角形则双曲线的离心率e= 。
=1(a>0,b>0)的右焦点为F,右准线l与两条渐近线交于P、Q两点,如果△PQF是直角三角形则双曲线的离心率e= 。 表示双曲线,则
表示双曲线,则 的取值范围是
的取值范围是