题目内容
【题目】
．
（1）若 
时， 
，求cos4x的值；
（2）将 
的图象向左移 
，再将各点横坐标伸长为原来的2倍，纵坐标不变，得y=g（x），若关于g（x）+m=0在区间 
上的有且只有一个实数解，求m的范围．
【答案】
（1）解： 
=（ 
sin2x，cos2x）， 
=（cos2x，﹣cos2x），
∴f（x）= + 
= sin2xcos2x﹣cos22x+
= 
sin4x﹣ cos4x﹣ +
=﹣cos（4x+ 
）=﹣ 
，
∴cos（4x+ ）= ；
又 
时，4x+ ∈（ 
，2π），
∴sin（4x+ ）=﹣ 
=﹣ 
，
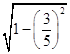∴cos4x=cos[（4x+ ）﹣ ]
=cos（4x+ ）cos +sin（4x+ 
）sin
= × +（﹣ ）×
= 
；
（2）解：由（1）知，f（x）= sin4x﹣ cos4x=sin（4x﹣ 
），
将f（x）的图象向左平移 
个单位，得y=sin[4（x+ ）﹣ ]=sin（4x+ ）的图象；
再将y各点横坐标伸长为原来的2倍，纵坐标不变，得y=sin（2x+ ）的图象；
则y=g（x）=sin（2x+ ）；
当x∈ 
时，2x+ ∈[ ， 
]，
画出函数g（x）的图象，如图所示；
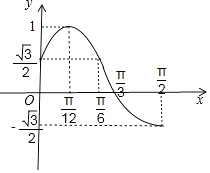
则g（x）+m=0在区间 上的有且只有一个实数解时，
应满足﹣ ≤﹣m＜ 或﹣m=1；
即﹣ ＜m≤ ，或m=﹣1．
【解析】（1）由题意，根据平面向量的数量积运算求出cos（4x+ 
）的值，再利用三角恒等变换求出cos4x的值；（2）由（1）知f（x）的解析式，利用图象平移和变换得出g（x）的解析式，画出函数g（x）的图象，结合图象求出m的取值范围．
练习册系列答案
优等生题库系列答案
相关题目
