Question

【题目】已知函数的图象与直线相切.

（1）求实数的值；

（2）函数，，若对任意的，恒成立，求实数的取值范围.

Answer 1

【答案】（1）1；（2）.

【解析】

（1）由，设切点为， 根据条件可得，，两式联立可得，设，讨论出函数的单调性，从而得出方程的根为，进而求出参数的值.
（2）对任意的，恒成立,即，令，则原问题等价于，讨论出函数的单调性，得出其最大值即可.

解：（1）设切点为，

所以函数的图象在点处的切线的斜率为

又

消得，令，得，

当时，，所以在区间单调递增，且，

又因为当时，，所以.

则，所以.

（2）即

即即.

令，则原问题等价于

，

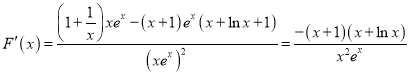令，则，

所以函数在上单调递增，

因为，，所以存在，使得，

所以当时，，；当时，，，

所以在上单调递增，在上单调递减，

由，得，即，所以

所以，

所以，故的取值范围为.