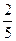题目内容
已知椭圆中心在原点,焦点在横轴上,焦距为4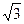 ,且和直线3x+2
,且和直线3x+2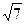 y-16=0相切,求椭圆方程.
y-16=0相切,求椭圆方程.
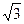 ,且和直线3x+2
,且和直线3x+2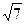 y-16=0相切,求椭圆方程.
y-16=0相切,求椭圆方程.椭圆的方程为 +
+ =1.
=1.
 +
+ =1.
=1.解法一:设椭圆方程为 =1(a>b>0),
=1(a>b>0),
切点为P(x0,y0),则切线为 ="1. " ①
="1. " ①
又切线为3x+2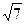 y-16="0, " ②
y-16="0, " ②
故直线①②重合.
∴ ,即x0=
,即x0= ,y0=
,y0= b2.
b2.
代入②,得9a2+28b2-256="0. " ③
又焦距为4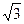 ,∴c=2
,∴c=2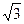 .
.
∴a2-b2="12. " ④
联立方程③④,解得
故所求椭圆的方程为 +
+ =1.
=1.
解法二:c=2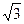 ,c2=12.
,c2=12.
设椭圆 =1与直线方程联立,Δ=0得b2=4.
=1与直线方程联立,Δ=0得b2=4.
故所求椭圆的方程为 +
+ =1.
=1.
 =1(a>b>0),
=1(a>b>0),切点为P(x0,y0),则切线为
 ="1. " ①
="1. " ①又切线为3x+2
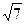 y-16="0, " ②
y-16="0, " ②故直线①②重合.
∴
 ,即x0=
,即x0= ,y0=
,y0= b2.
b2.代入②,得9a2+28b2-256="0. " ③
又焦距为4
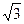 ,∴c=2
,∴c=2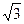 .
.∴a2-b2="12. " ④
联立方程③④,解得

故所求椭圆的方程为
 +
+ =1.
=1.解法二:c=2
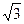 ,c2=12.
,c2=12.设椭圆
 =1与直线方程联立,Δ=0得b2=4.
=1与直线方程联立,Δ=0得b2=4.故所求椭圆的方程为
 +
+ =1.
=1.
练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
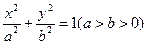 的离心率
的离心率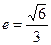 ,
, 为过点
为过点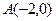 和上顶点
和上顶点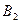 的直线,下顶点
的直线,下顶点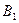 与
与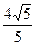 .
.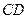 交
交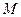 , 若
, 若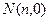 ,试求
,试求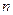 的范围.
的范围.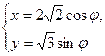 (φ为参数)上一点M与原点的连线与x轴正方向所成角为
(φ为参数)上一点M与原点的连线与x轴正方向所成角为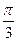 ,求点M的坐标.
,求点M的坐标. +
+ =1,若它的一条弦AB被M(1,1)平分,则AB所在的直线方程为________.
=1,若它的一条弦AB被M(1,1)平分,则AB所在的直线方程为________.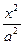 +
+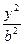 =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e=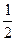 ,左焦点为F,A、B、C为其三个顶点,直线CF与AB交于D,则tan∠BDC的值等于( )
,左焦点为F,A、B、C为其三个顶点,直线CF与AB交于D,则tan∠BDC的值等于( )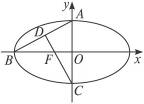
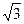 B.-3
B.-3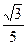 D.-
D.-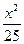 +
+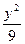 =1上一点P到两焦点距离之积为m,则m最大时求P点坐标.
=1上一点P到两焦点距离之积为m,则m最大时求P点坐标. +
+ =1的两个焦点,P是椭圆上一点,且|PF1|-|PF2|=1,则cos∠F1PF2=___________.
=1的两个焦点,P是椭圆上一点,且|PF1|-|PF2|=1,则cos∠F1PF2=___________.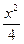 +y2=1相交于A、B两点,则|AB|的最大值是( )
+y2=1相交于A、B两点,则|AB|的最大值是( )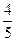
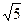 C.
C.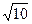 D.
D.