题目内容
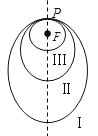
【题目】如图所示，某公园内有两条道路
，
，现计划在上选择一点
，新建道路
，并把
所在的区域改造成绿化区域．已知
，
．
（1）若绿化区域的面积为1
，求道路的长度；
（2）若绿化区域改造成本为10万元/，新建道路成本为10万元/．设
（
），当
为何值时，该计划所需总费用最小？
【答案】（1）
（2）
【解析】
（1）由
的面积可得
，结合余弦定理可得结果.
（2）在中利用正弦定理可得
，
．从而得到总费用
．利用导数研究最值即可.
（1）因为在中，已知
，
，
所以由的面积
，
解得．
在中，由余弦定理得：
，
所以
．
（2）由
，则
，
．
在中，， ，由正弦定理得
，
所以，．
记该计划所需费用为
，
则
．
令
，则
，
由
，得．所以当
时，
，
单调递减；
当
时，
，单调递增．
所以时，该计划所需费用最小．
练习册系列答案
应用题天天练四川大学出版社系列答案
相关题目
