题目内容
证明不等式: <
<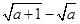 ,其中a≥0.=
,其中a≥0.=
 <
<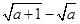 ,其中a≥0.=
,其中a≥0.=用分析法证明。
试题分析:要证
 <
<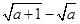 成立,
成立,需证
 <
<
需证
 >
>
因为
 显然成立,所以原命题成立。
显然成立,所以原命题成立。点评:容易题,利用分析法证明不等式,从格式上来说,表述要规范。本题也可转化证明
 <
< ,两边平方。
,两边平方。
练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
题目内容
 <
<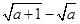 ,其中a≥0.=
,其中a≥0.= <
<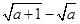 成立,
成立, <
<
 >
>
 显然成立,所以原命题成立。
显然成立,所以原命题成立。 <
< ,两边平方。
,两边平方。
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案