题目内容
切线 与圆切于点
与圆切于点 ,圆内有一点
,圆内有一点 满足
满足 ,
, 的平分线
的平分线 交圆于
交圆于 ,
, ,延长
,延长 交圆于
交圆于 ,延长
,延长 交圆于
交圆于 ,连接
,连接 .
.
(Ⅰ)证明: //
// ;
;
(Ⅱ)求证: .
.
(Ⅰ)详见解析;(Ⅱ)详见解析.
解析试题分析:(Ⅰ)证明: //
// ,只需证明
,只需证明 ,而
,而 ,即证
,即证 ,只需证△
,只需证△ ∽△
∽△ ,即可,由已知切线
,即可,由已知切线 与圆切于点
与圆切于点 ,圆内有一点
,圆内有一点 满足
满足 ,
, 的平分线
的平分线 交圆于
交圆于 ,
, ,由切割线定理知
,由切割线定理知 ,从而得
,从而得 ,故△
,故△ ∽△
∽△ ,从而得证;(Ⅱ)连接
,从而得证;(Ⅱ)连接 ,求证:
,求证: ,注意到△
,注意到△ △
△ ,可得
,可得 ,只需证
,只需证 ,即证
,即证 ,即证△
,即证△ △
△ ,这容易证出.
,这容易证出.
试题解析:(Ⅰ)证明:∵ 切圆于
切圆于 ,∴
,∴ ,又∵
,又∵ ,∴
,∴ ,∴△
,∴△ ∽△
∽△ ,∴
,∴ ,又∵
,又∵ ,∴
,∴ ,∴
,∴ //
// ;
;
(Ⅱ)证明:连接 ,由
,由 ,
, 及
及 ,知△
,知△ △
△ ,同理有△
,同理有△ △
△ ,∴
,∴ ,故
,故 ,又
,又 ,∴
,∴ .
.
考点:割线定理、相似三角形、等角对等弦.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
相关题目

 内接于
内接于 上,
上, ,
, 交
交 于点E,点F在DA的延长线上,
于点E,点F在DA的延长线上, ,求证:
,求证:
 是
是 .
.
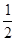 ,⊙O的半径为3,求OA的长.
,⊙O的半径为3,求OA的长. 与⊙
与⊙ 相切,
相切, 为切点,
为切点, 为割线,弦
为割线,弦 ,
, 相交于
相交于 点,
点, 为
为 上一点,且
上一点,且 .
.
 ;
; .
. ,且AB是的
,且AB是的
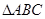 中,
中,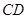 是
是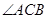 的角平分线,
的角平分线, 的外接圆交
的外接圆交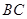 于
于 ,
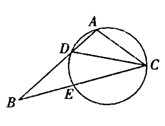
,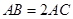 .
.
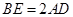 ;
;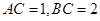 时,求
时,求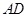 的长.
的长.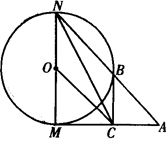
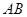 是圆
是圆 的直径,
的直径,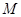 为圆上一点,
为圆上一点, ,垂足为
,垂足为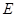 ,点
,点 为圆
为圆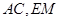 交于点
交于点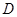 ,
,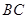 交
交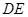 于点
于点 .
.
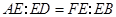 ;(2)
;(2)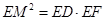 .
.