题目内容
已知映射f:A→B,其中B=R,对应法则:f:x→y=log0.5(2-x)-
,对于实数k∈B,在集合A中不存在原象,则k的取值范围是( )
| 1-x |
| A、k>0 | B、k<1 |
| C、k<0 | D、以上都不对 |
考点:映射
专题:计算题,函数的性质及应用
分析:实数k∈B,在集合A中不存在原象,表示k应该在A中所有元素在B中对应象组成的集合的补集中,故我们可以根据已知条件中的A,映射f:A→B,对应法则为f:x→y=log0.5(2-x)-
,求出A中所有元素在B中对应的象组成的集合,再求其补集即可得到答案.
| 1-x |
解答:
解:由于y=log0.5(2-x)-
,则其定义域为A={x|2-x>0且1-x≥0}={x|x≤1},
由于x≤1,则2-x≥1,1-x≥0,
故log0.5(2-x)≤0,
≥0,
则当x∈A时,在映射f:A→B的作用下对应象的满足:y≤0.,
故若实数k∈B,在集合A中不存在原象,则k应满足,k>0
即满足条件的实数k的取值范围是k>0.
故选:A.
| 1-x |
由于x≤1,则2-x≥1,1-x≥0,
故log0.5(2-x)≤0,
| 1-x |
则当x∈A时,在映射f:A→B的作用下对应象的满足:y≤0.,
故若实数k∈B,在集合A中不存在原象,则k应满足,k>0
即满足条件的实数k的取值范围是k>0.
故选:A.
点评:在集合A到B的映射中,若存在实数k∈B,在集合A中不存在原象,表示k应该在A中所有元素在B中对应象组成的集合的补集中.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
如果M={x|x+1>0},则( )
| A、∅∈M | B、0?M |
| C、{0}∈M | D、{0}⊆M |
方程根用二分法来求可谓是“千呼万唤始出来、犹抱琵琶半遮面”.若函数f(x)在区间(1,2)内有一个零点,用“二分法”求该函数的零点的近似值,使其具有5位有效数字,则至少需要将区间(1,2)等分( )
| A、12次 | B、13次 |
| C、14次 | D、16次 |
某工厂的生产流水线每小时可生产产品100件,这一天开始生产前没有产品积压,生产3小时后,工厂派来装御工装相,每小时装产品150件,则从开始装箱时起,未装箱的产品数量y与时间t之间的关系图象大概是( )
A、 |
B、 |
C、 |
D、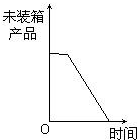 |
 一个简单几何体的主视图、侧视图如图所示,则其俯视图不可能为 ①长、宽不相等的长方形;②正方形;③圆;④椭圆.其中正确的是( )
一个简单几何体的主视图、侧视图如图所示,则其俯视图不可能为 ①长、宽不相等的长方形;②正方形;③圆;④椭圆.其中正确的是( )| A、①② | B、②③ | C、③④ | D、①④ |