题目内容
某工厂的生产流水线每小时可生产产品100件，这一天开始生产前没有产品积压，生产3小时后，工厂派来装御工装相，每小时装产品150件，则从开始装箱时起，未装箱的产品数量y与时间t之间的关系图象大概是（ ）
A、 |
B、 |
C、 |
D、 |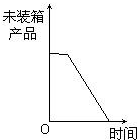
考点：函数的图象
专题：函数的性质及应用
分析：前三个小时是生产时间，所以未装箱的产品的数量是增加的，后开始装箱，每小时装的产品比每小时生产的产品数量多，所以未装箱的产品数量是下降的，直至0．
解答：
解：∵前三个小时是生产时间，
∴未装箱的产品的数量是增加的，
∵后开始装箱，每小时装的产品比每小时生产的产品数量多，
∴未装箱的产品数量是下降的，直至0．
∴表现在图象上为随着时间的增加，未装箱的产品的图象是先上升后下降至0的．
故选：B．
∴未装箱的产品的数量是增加的，
∵后开始装箱，每小时装的产品比每小时生产的产品数量多，
∴未装箱的产品数量是下降的，直至0．
∴表现在图象上为随着时间的增加，未装箱的产品的图象是先上升后下降至0的．
故选：B．
点评：本题考查的实际生活中函数的图形变化，根据题意判断函数图形的大致走势，比较简单．
练习册系列答案
相关题目
如图所示，在平面直角坐标系xOy中，角α，β的顶点与坐标原点重合，始边与x轴的非负半轴重合，它们的终边分别与单位圆相交于A，B两点．若点A，B的坐标分别为（设集合A{（m，n）|0＜m＜2，0＜n＜2，m，n∈R}，则任取（m，n）∈A，关于x的方程
x2+nx+m=0有实根的概率为（ ）
| m |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
在各项都为正数的等比数列{an}中，首项a1=3，前三项和为S3=21，则a4=（ ）
| A、32 | B、24 | C、27 | D、54 |
已知数列{an}为等差数列，其前n项和为Sn，若S4=20，S6-S2=36，则该等差数列的公差d=（ ）
| A、-2 | B、2 | C、-4 | D、4 |
已知映射f：A→B，其中B=R，对应法则：f：x→y=log0.5（2-x）-
，对于实数k∈B，在集合A中不存在原象，则k的取值范围是（ ）
| 1-x |
| A、k＞0 | B、k＜1 |
| C、k＜0 | D、以上都不对 |
有若干个边长为1的小正方体搭成一个几何体，这个几何体的主视图和右视图均如图所示，那么符合这个平面图形的小正方体块数最多时该几何体的体积是（ ）