题目内容
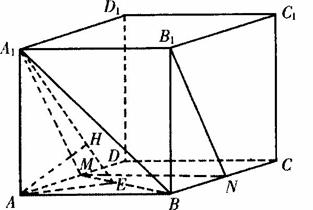
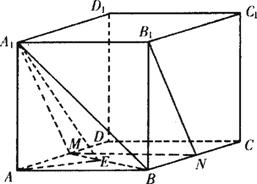
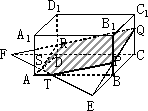
如图,已知在长方体ABCD-A1B1C1D1中,P,Q,R分别为棱BB1,CC1,DD1上的点,且QP不平行于BC,QR不平行于CD.试画出过P,Q,R三点的截面.
答案:
解析:
解析:
分析:要画出过P,Q,R三点的截面,只要画出平面PQR与平面ABB1A1和平面ADD1A1的交线即可.
解:延长QP交CB的延长线于点E,延长QR交CD的延长线于点F,
则E∈平面PQR,F∈平面PQR.
所以EF![]() 平面PQR.
平面PQR.
连接EF,交AB于点T,交AD于点S,连接RS,TP.
因为S,T∈EF,EF![]() 平面PQR,
平面PQR,
所以S,T∈平面PQR.
故SR![]() 平面PQR,TP
平面PQR,TP![]() 平面PQR,即SR,TP分别为平面PQR与平面ADD1A1和平面ABB1A1的交线.
平面PQR,即SR,TP分别为平面PQR与平面ADD1A1和平面ABB1A1的交线.
所以多边形PQRST即为所求的截面.
点评:多面体的截面是由平面与多面体表面的交线围成的平面多边形,故作出截面的关键是作出平面与多面体表面的交线,不可简单地将P,Q,R三点连接起来得截面.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
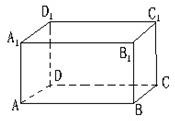 已知如图:长方体ABCD-A1B1C1D1中,交于顶点A的三条棱长别为AD=3,AA1=4,AB=5.一天,小强观察到在A处有一只蚂蚁,发现顶点C1处有食物,于是它沿着长方体的表面爬行去获取食物,则蚂蚁爬行的最短路程是( )
已知如图:长方体ABCD-A1B1C1D1中,交于顶点A的三条棱长别为AD=3,AA1=4,AB=5.一天,小强观察到在A处有一只蚂蚁,发现顶点C1处有食物,于是它沿着长方体的表面爬行去获取食物,则蚂蚁爬行的最短路程是( )