题目内容
向量
=(x,y),
=(x2,y2),
=(1,1),
=(2,2),若
•
=
•
=1,则这样的向量
有多少个 .
| a |
| b |
| c |
| d |
| a |
| c |
| b |
| d |
| a |
考点:平面向量数量积的坐标表示、模、夹角
专题:平面向量及应用
分析:根据平面向量的坐标运算,列出方程组,求出解即可得出结论.
解答:
解:∵
•
=
•
=1,
∴1•x+1•y=2•x2+2•y2=1,
即
;
解得
,
∴
=(1,1),只有一个.
故答案为:一个.
| a |
| c |
| b |
| d |
∴1•x+1•y=2•x2+2•y2=1,
即
|
解得
|
∴
| a |
故答案为:一个.
点评:本题考查了平面向量的应用问题,解题时应根据平面向量的坐标运算来解答,是基础题.

练习册系列答案
相关题目
如图是函数y=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<
)的图象,则其解析式是( )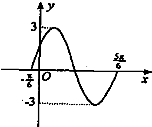
| π |
| 2 |

A、y=3sin(2x+
| ||
B、y=3sin(2x+
| ||
C、y=3sin(2x-
| ||
D、y=3sin(2x+
|
若命题p为真,命题q为假,则( )
| A、命题“p∧q”为真 |
| B、命题“p∨q”为真 |
| C、命题“¬p”为真 |
| D、命题“¬q”为假 |
已知递增等差数列{an}中,a6=18且a2是a1,a4的等比中项,则它的第4项到第11项的和为( )
| A、180 | B、198 |
| C、189 | D、168 |
已知函数y=x+2,则y′=( )
| A、x | B、x+2 | C、1 | D、2 |
设函数f(x)=
sin2x-
cos2x,以下关于f(x)的说法正确的是( )
| ||
| 2 |
| 1 |
| 2 |
A、其图象可由 y=sin2x向右平移
| ||
B、其图象关于直线x=
| ||
C、其图象关于点(
| ||
D、在区间(-
|
下列函数:y=x,y=x3,y=
,y=x3-x是奇函数的有( )
| 1 |
| x |
| A、1个 | B、2个 | C、3个 | D、4个 |