题目内容

4．已知集合A={x|3x+3＜1}，B={x|x2-4x-12＞0}，则（∁RA）∩B=（　　）
A．[-3，-2）B．（-∞，-3]C．[-3，-2）∪（6，+∞）D．（-3，-2）∪（6，+∞）

分析 先分别求出集合A，B，从而求出CRA，由此能求出（∁RA）∩B．

解答 解：∵集合A={x|3x+3＜1}={x|x＜-3}，
B={x|x2-4x-12＞0}={x|x＜-2或x＞6}，
∴CRA={x|x≥-3}，
（∁RA）∩B=[-3，-2）∪（6，+∞）．
故选：C．

点评 本题考查交集的求法，是基础题，解题时要认真审题，注意补集、交集定义的合理运用．

练习册系列答案
相关题目
14．已知函数f（x）=ax+x2-xlna（a＞1），x∈[-1，1]．
（1）证明：f（0）是f（x）的极小值；
（2）对任意x1，x2∈[-1，1]，使得|f（x1）-f（x2）|≤e-1，求实数a的取值范围．
15．已知函数f（x）=cos（2x+$\frac{π}{3}$），若存在x1，x2，…xn满足0≤x1＜x2＜…＜xn≤4π，且|f（x1）-f（x2）|+|f（2）-f（x3）|+…+|f（xn-1）-f（xn）|=16（n≥2，n∈N*），则n的最小值为（　　）
A．8B．9C．10D．11
12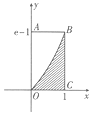．图所示的阴影部分由坐标轴、直线x=1及曲线y=ex-lne围成，现向矩形区域OABC内随机投掷一点，则该点落在非阴影区域的概率是（　　）
A．$\frac{1}{e}$B．$\frac{1}{e-1}$C．1-$\frac{1}{e}$D．1-$\frac{1}{e-1}$
19．已知等比数列{an}为递增数列，若a1＞0，且2（an+2-an）=3an+1，则数列{an}的公比q=（　　）
A．2或$\frac{1}{2}$B．2C．$\frac{1}{2}$D．-2
9．已知集合A={x|1＜x2＜4}，B={x|x-1≥0}，则A∩B=（　　）
A．（1，2）B．[1，2）C．（-1，2）D．[-1，2）
16．锐角△ABC中，内角A，B，C的对边分别为a，b，c，且满足（a-b）（sinA+sinB）=（c-b）sinC，若$a=\sqrt{3}$，则b2+c2的取值范围是（　　）
A．（5，6]B．（3，5）C．（3，6]D．[5，6]
7．在△ABC中，$AB=\sqrt{7}$，BC=3，∠C=60°，则AC=1或2．
8．在一次“对学生的数学成绩与物理成绩是否有关”的独立性检验的试验中，由2×2列联表算得K2的观测值k≈7.813，参照附表判断，在此次试验中，下列结论正确的是（　　）   
附表：
P（K2≥k）0.0500.0100.001
k3.8416.63510.828
A．在犯错误的概率不超过0.001的前提下，认为“数学成绩与物理成绩有关”
B．在犯错误的概率不超过0.01的前提下，认为“数学成绩与物理成绩有关”
C．有99%以上的把握认为“数学成绩与物理成绩无关”
D．有99.9%以上的把握认为“数学成绩与物理成绩有关”

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网