题目内容
14.已知函数f(x)=ax+x2-xlna(a>1),x∈[-1,1].(1)证明:f(0)是f(x)的极小值;
(2)对任意x1,x2∈[-1,1],使得|f(x1)-f(x2)|≤e-1,求实数a的取值范围.
分析 (1)求出f′(x),判断f′(x)在(-1,0)和(0,1)上的符号即可得出结论;
(2)求出f(x)在[-1,1]上的最值,令fmax(x)-fmin(x)≤e-1得出关于a的不等式a-lna≤e-1,再根据F(a)=a-lna的单调性得出a的范围.
解答 (1)证明:f′(x)=axlna+2x-lna=(ax-1)lna+2x,
∴f′(0)=0,
∵a>1,
∴当x∈(-1,0)时,(ax-1)<0,lna>0,2x<0,
∴f′(x)=(ax-1)lna+2x<0,
当x∈(0,1)时,(ax-1)>0,lna>0,2x>0,
∴f′(x)=(ax-1)lna+2x>0,
∴f(x)在(-1,0)上单调递减,在(0,1)上单调递增,
∴f(0)是f(x)的极小值.
(2)解:由(1)可知f(x)在(-1,0)上单调递减,在(0,1)上单调递增,
∴fmin(x)=f(0)=1,
又f(-1)=$\frac{1}{a}$+1+lna,f(1)=a+1-lna,
令h(a)=f(-1)-f(1)=$\frac{1}{a}-a+2lna$,则h′(a)=-$\frac{1}{{a}^{2}}$-1+$\frac{2}{a}$=$\frac{-{a}^{2}+2a-1}{{a}^{2}}$=-$\frac{(a-1)^{2}}{{a}^{2}}$<0,
∴h(a)在(1,+∞)上单调递减,
∴h(a)=f(-1)-f(1)<h(1)=0,即f(-1)<f(1),
∴fmax(x)=f(1)=a+1-lna.
∴对于任意x1,x2∈[-1,1],使得|f(x1)-f(x2)|≤f(1)-f(0)=a-lna,
∴a-lna≤e-1恒成立,
令F(a)=a-lna,则F′(a)=1-$\frac{1}{a}$>0,
∴F(a)在(1,+∞)上是增函数,且F(e)=e-1,
∴1<a≤e.
点评 本题考查了导数与函数单调性、极值、最值的关系,属于中档题.

 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案| 分数区间 | [50,70] | [70,90] | [90,110] | [110,130] | [130,150] |
| 人数 | 2 | 8 | 32 | 38 | 20 |
(2)现从成绩在[70,110)中按照分数段,采取分成抽样的方法随机抽取5人,再在这5人中随机抽取2人作小题得分分析,求恰有1人的成绩在[70,90)上的概率.
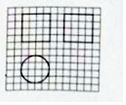 如图,网络纸上正方形小格的边长为1,图中粗线画出的是某几何体毛坯的三观图,切削该毛坯得到一个表面积最大的长方体,则该长方体的表面积为( )
如图,网络纸上正方形小格的边长为1,图中粗线画出的是某几何体毛坯的三观图,切削该毛坯得到一个表面积最大的长方体,则该长方体的表面积为( )| A. | 24 | B. | 16+32$\sqrt{2}$ | C. | 16+8$\sqrt{2}$ | D. | 32 |
| A. | 1050辆 | B. | 1350辆 | C. | 1650辆 | D. | 1950辆 |
| A. | 4 | B. | 5 | C. | $\frac{4}{5}$ | D. | 与点P的位置有关 |
| A. | [-3,-2) | B. | (-∞,-3] | C. | [-3,-2)∪(6,+∞) | D. | (-3,-2)∪(6,+∞) |
 如图,点C是以AB为直径的圆上一点,直角梯形BCDE所在平面与圆O所在平面垂直,且DE∥BC,DC⊥BC,DE=$\frac{1}{2}$BC=2,AC=CD=3.
如图,点C是以AB为直径的圆上一点,直角梯形BCDE所在平面与圆O所在平面垂直,且DE∥BC,DC⊥BC,DE=$\frac{1}{2}$BC=2,AC=CD=3.