题目内容
7.如图,△ABC的内切圆I与边AB、AC分别切于点D、E,O为△BCI的外心.证明:∠ODB=∠OEC.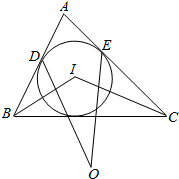
分析 证明A,B,O,C 四点共圆,△OAD≌△OAE,即可证明结论.
解答 证明:由O是△BCI的外心,知∠BOI=2∠BCI=∠BCA.同理,∠COI=∠CBA.
则∠BOC=∠BOI+∠COI=∠BCA+∠CBA=180°-∠BAC.
于是,A,B,O,C 四点共圆.
由OB=OC,知∠BAO=∠CAO.
因为AD=AE,AO=AO,
所以,△OAD≌△OAE.因此,∠ODA=∠OEA.
故∠ODB=∠OEC.
点评 本题考查四点共圆,三角形全等的证明,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
15.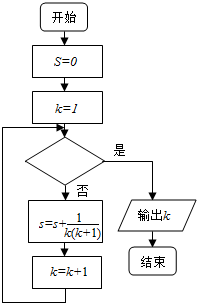 运行如图所示的程序框图,若输出结果为$\frac{6}{7}$,则判断框中应该填的条件是( )
运行如图所示的程序框图,若输出结果为$\frac{6}{7}$,则判断框中应该填的条件是( )
 运行如图所示的程序框图,若输出结果为$\frac{6}{7}$,则判断框中应该填的条件是( )
运行如图所示的程序框图,若输出结果为$\frac{6}{7}$,则判断框中应该填的条件是( )| A. | k>5 | B. | k>6 | C. | k>7 | D. | k>8 |
2.执行下面的程序框图,则输出的m的值为( )
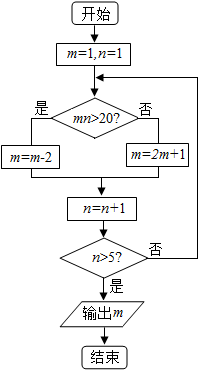

| A. | 9 | B. | 7 | C. | 5 | D. | 11 |