题目内容

17．设函数f（x）=$\left\{\begin{array}{l}{{x}^{2}+1，x≤1}\\{\frac{2}{x}，x＞1}\end{array}\right.$，则f（f（3））=$\frac{13}{9}$，方程f（f（x））=$\frac{1}{4}$的解集为-$\sqrt{7}$．

分析 根据已知中函数f（x）=$\left\{\begin{array}{l}{{x}^{2}+1，x≤1}\\{\frac{2}{x}，x＞1}\end{array}\right.$，将x=3代入可得f（f（3）），再由f（f（x））=$\frac{1}{4}$，可求出满足条件的x值．

解答 解：∵函数f（x）=$\left\{\begin{array}{l}{{x}^{2}+1，x≤1}\\{\frac{2}{x}，x＞1}\end{array}\right.$，
∴f（f（3））=f（$\frac{2}{3}$）=$\frac{13}{9}$，
∵f（f（x））=$\frac{1}{4}$＜2，
∴f（x）＞1，
则$\frac{2}{f（x）}=\frac{1}{4}$，
故f（x）=8，
∵f（x）=8＞2，
故x≤1，
故x2+1=8，
解得：x=-$\sqrt{7}$
故答案为：$\frac{13}{9}$，{-$\sqrt{7}$}

点评 本题考查的知识点是分段函数的应用，函数求值，分类讨论思想，难度中档．

练习册系列答案
相关题目
7．如图，△ABC的内切圆I与边AB、AC分别切于点D、E，O为△BCI的外心．证明：∠ODB=∠OEC．
8．已知函数f（x）的定义域为（0，+∞），并且满足三个条件：①对任意的x，y∈R+，都有f（x+y）=f（x）f（y）；②对任意的x∈R+，都有0＜f（x）＜1；③f（2）=$\frac{1}{4}$．
（Ⅰ）求f（1），f（3）的值；
（Ⅱ）证明：函数f（x）为区间（0，+∞）上的减函数；
（Ⅲ）解不等式：f（2x）＜$\frac{1}{32}$f（-x2+6x-8）．
5．对任意非零实数a，b，定义a?b的算法原理如程序框图所示．设a为函数y=x2-2x+3（x∈R）的最小值，b为抛物线y2=8x的焦点到准线的距离，则计算机执行该运算后输出结果是（　　）
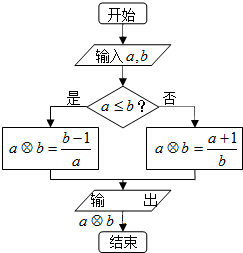
A．$\frac{2}{3}$B．$\frac{3}{2}$C．$\frac{7}{2}$D．$\frac{1}{2}$
12．下列推理错误的是（　　）
A．A∈l，A∈α，B∈l，B∈α⇒l?αB．A∈α，A∈β，B∈α，B∈β⇒α∩β=AB
C．l?α，A∈l⇒A∉αD．A∈l，l?α⇒A∈α
2．已知双曲线$\frac{{x}^{2}}{m}$-y2=1（m＞0）的离心率为$\frac{2\sqrt{3}}{3}$，则m的值为（　　）
A．$\frac{2\sqrt{3}}{3}$B．3C．8D．$\frac{\sqrt{3}}{2}$
9．已知田径队有男运动员36人，女运动员24人，若用分层抽样的方法从该队的全体运动员中抽取一个容量为20的样本，则抽取男运动员的人数为（　　）
A．9B．12C．15D．16
6．定义：若对定义域D内的任意两个x1，x2（x1≠x2），均有|f（x1）-f（x2）|＜|x1-x2|成立，则称函数y=f（x）是D上的“平缓函数”．则以下说法正确的有（　　）
①f（x）=-lnx+x为（0，+∞）上的“平缓函数”
②g（x）=sinx为R上的“平缓函数”
③h（x）=x2-x是为R上的“平缓函数”
④已知函数y=k（x）为R上的“平缓函数”，若数列{an}对?n∈N*总有|xn+1-xn|≤$\frac{1}{（2n+1）^{2}}$，则k（xn+1）-k（x1）＜$\frac{1}{4}$．
A．0个B．1个C．2个D．3个
7．已知幂函数f（x）的图象经过点（$\sqrt{3}$，3），则f（2）的值是（　　）
A．4B．2C．$\frac{1}{4}$D．$\frac{1}{2}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网