题目内容
16.变量 x、y满足线性约束条件$\left\{\begin{array}{l}{3x+y-2≤0}\\{y-x≤2}\\{y≥x-1}\end{array}\right.$,则目标函数z=(k+1)x-y,仅在点(0,2)取得最小值,则k的取值范围是( )| A. | k<-4 | B. | -4<k<0> | C. | -2<k<0 | D. | k>0 |
分析 由约束条件作出可行域,化目标函数为直线方程的斜截式,结合目标函数z=(k+1)x-y仅在点(0,2)取得最小值列式求得k值.
解答  解:由约束条件$\left\{\begin{array}{l}{3x+y-2≤0}\\{y-x≤2}\\{y≥x-1}\end{array}\right.$作出可行域如图,
解:由约束条件$\left\{\begin{array}{l}{3x+y-2≤0}\\{y-x≤2}\\{y≥x-1}\end{array}\right.$作出可行域如图,
∵目标函数z=(k+1)x-y,仅在点(0,2)取得最小值,
∴-3<k+1<1,即-4<k<0.
故选:B.
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
6.双曲线$\frac{x^2}{9}-\frac{y^2}{16}=1$的右焦点坐标为( )
| A. | (5,0) | B. | (0,5) | C. | ($\sqrt{7}$,0) | D. | (0,$\sqrt{7}$) |
5.对任意非零实数a,b,定义a?b的算法原理如程序框图所示.设a为函数y=x2-2x+3(x∈R)的最小值,b为抛物线y2=8x的焦点到准线的距离,则计算机执行该运算后输出结果是( )
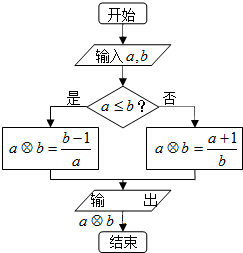

| A. | $\frac{2}{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{7}{2}$ | D. | $\frac{1}{2}$ |