题目内容
设a>0且a≠1,则“函数f(x)=ax在R上是减函数”,是“函数g(x)=(2﹣a)x3在R上是增函数”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
A
解析

练习册系列答案
 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
下列有关命题的说法中错误的是
A.若“ ”为真命题,则 ”为真命题,则 、 、 均为真命题 均为真命题 |
B.若命题 “ “ , , ”则命题 ”则命题 为“ 为“ , , ” ” |
C.“ ”是“ ”是“ ”的充分不必要条件 ”的充分不必要条件 |
D.“ ”的必要不充分条件是“ ”的必要不充分条件是“ ” ” |
已知命题p:若x>0且y>0,则xy>0,则p的否命题是( )
| A.若x>0且y>0,则xy≤0 |
| B.若x≤0且y≤0,则xy≤0 |
| C.若x,y至少有一个不大于0,则xy<0 |
| D.若x,y至少有一个小于或等于0,则xy≤0 |
①若“p q”为真命题,则p、q均为真命题( );
q”为真命题,则p、q均为真命题( );
②“若 ”的否命题为“若
”的否命题为“若 ,则
,则 ”;
”;
③“ ”的否定是“
”的否定是“ ”;
”;
④“ ”是“
”是“ ”的充要条件. 其中不正确的命题是
”的充要条件. 其中不正确的命题是
| A.①② | B.②③ | C.①③ | D.③④ |
德国著名数学家狄利克雷在数学领域成就显著,以其名命名的函数
被称为狄利克雷函数,其中 为实数集,
为实数集, 为有理数集,则关于函数
为有理数集,则关于函数 有如下四个命题:
有如下四个命题:
① ; ②函数
; ②函数 是偶函数;
是偶函数;
③任取一个不为零的有理数 ,
, 对任意的
对任意的 恒成立;
恒成立;
④存在三个点 ,使得
,使得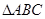 为等边三角形.
为等边三角形.
其中真命题的个数是( )
| A.1 | B.2 | C.3 | D.4 |
已知命题 ,使
,使 为偶函数;命题
为偶函数;命题
 ,则下列命题中为真命题的是( )
,则下列命题中为真命题的是( )
A. | B. | C. | D. |
对于函数y=f(x),x∈R,“y=|f(x)|的图象关于y轴对称”是“y=f(x)是奇函数”的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
下面四个条件中,使a>b成立的充分而不必要的条件是( )
| A.a>b+1 | B.a>b﹣1 | C.a2>b2 | D.a3>b3 |
若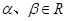 ,且
,且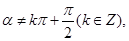
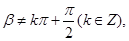 则“
则“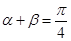 ”是“
”是“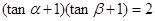 ”的( )
”的( )
| A.充分不必要条件 |
| B.必要不充分条件 |
| C.充要条件 |
| D.既不充分也不必要 |