题目内容
已知命题
，使
为偶函数；命题
，则下列命题中为真命题的是（ ）
A． | B． | C． | D． |
Ｃ
解析试题分析：当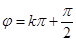
时，函数
是偶函数，故命题
是真命题；
，故命题
是假命题，故选C．
考点：复合命题的真假判断.
练习册系列答案
相关题目
已知命题p：“?x∈[1,2]，x2－a≥0”；命题q：“?x∈R，x2＋2ax＋2－a＝0”．若命题“p且q”是真命题，则实数a的取值范围为( )
| A．a≤－2或a＝1 |
| B．a≤－2或1≤a≤2 |
| C．a≥1 |
| D．－2≤a≤1 |
已知命题p：?x1，x2∈R，(f(x2)－f(x1))(x2－x1)≥0，则¬p是( )
| A．?x1，x2∈R，(f(x2)－f(x1))(x2－x1)≤0 |
| B．?x1，x2∈R，(f(x2)－f(x1))(x2－x1)≤0 |
| C．?x1，x2∈R，(f(x2)－f(x1))(x2－x1)<0 |
| D．?x1，x2∈R，(f(x2)－f(x1))(x2－x1)<0 |
的图像关于直线
对称，q：函数
的图像关于点
对称，则下列命题中的真命题为（ ）
已知空间直线
不在平面
内，则“直线上有两个点到平面的距离相等”是“
”的( )．
| A．充分非必要条件 | B．必要非充分条件 | C．充要条件 | D．非充分非必要条件 |
“
”是“函数
存在零点”的
| A．充分不必要条件 | B．必要不充分条件 |
| C．充要条件 | D．既不充分又不必要条件 |
若命题“
”为真命题，则（ ）
A． 均为真命题 | B．中至少有一个为真命题 |
| C．中至多有一个为真命题 | D．均为假命题 |
设a＞0且a≠1，则“函数f（x）=ax在R上是减函数”，是“函数g（x）=（2﹣a）x3在R上是增函数”的（ ）
| A．充分不必要条件 | B．必要不充分条件 |
| C．充分必要条件 | D．既不充分也不必要条件 |
若p：
,q:f(x)=sin(
)(
)是偶函数，则p是q的（ ）
| A．充要条件 | B．充分不必要条件 |
| C．必要不充分条件 | D．既不充分也不必要条件 |