题目内容
已知函数 ,
, .
.
(I)讨论函数 的单调性;
的单调性;
(Ⅱ)当 时,
时, ≤
≤ 恒成立,求
恒成立,求 的取值范围.
的取值范围.
(I) ,
, 在
在 单调递增;
单调递增; ,
, 在
在 单调递增,
单调递增, 单调递减.
单调递减.
(Ⅱ) .
.
解析试题分析:(I)根据单调函数的性质,分 ,
, 讨论
讨论 的单调性,即可得到结论.
的单调性,即可得到结论.
(Ⅱ)注意到“当 时,
时, ≤
≤ 恒成立”,等价于
恒成立”,等价于 在
在 恒成立,因此,通过确定
恒成立,因此,通过确定 ,分以下三种情况讨论:
,分以下三种情况讨论: ,
, ,
, ,得出结论:
,得出结论: . 12分
. 12分
试题解析:(I) ,
, 在
在 单调递增
单调递增 ,
, 在
在 单调递增,
单调递增, 单调递减 6分
单调递减 6分
(Ⅱ)等价于 在
在 恒成立,
恒成立,
(1)当 时,
时, ,所以
,所以 在
在 单调递增,
单调递增, ,与题意矛盾
,与题意矛盾
(2)当 时,
时, 恒成立,所以
恒成立,所以 在
在 单调递减,所以
单调递减,所以
(3)当 时,
时, ,所以
,所以 在
在 单调递增,
单调递增, ,与题意矛盾,综上所述:
,与题意矛盾,综上所述: 12分
12分
考点:函数的单调性,应用导数研究函数的极值.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
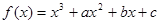 ,过曲线
,过曲线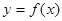 上的点
上的点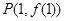 的切线方程为
的切线方程为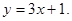 .
. 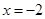 时有极值,求
时有极值,求 的表达式;
的表达式;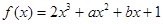 的导数为
的导数为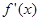 ,若函数
,若函数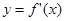 的图象关于直线
的图象关于直线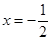 对称,且函数
对称,且函数 在
在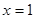 处取得极值.
处取得极值.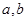 的值;
的值;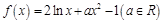 .
. 的单调区间;
的单调区间;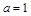 ,试解答下列两小题.
,试解答下列两小题.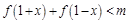 对任意的
对任意的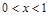 恒成立,求实数
恒成立,求实数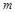 的取值范围;
的取值范围;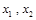 是两个不相等的正数,且以
是两个不相等的正数,且以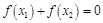 ,求证:
,求证: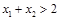 .
. ,函数
,函数 .
. ,求曲线
,求曲线 在点
在点 处的切线方程;
处的切线方程; 的单调区间;
的单调区间; 时,求函数
时,求函数 上的最小值.
上的最小值.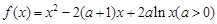 .
. 时,求曲线
时,求曲线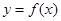 在点
在点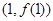 处的切线方程;
处的切线方程;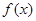 的单调区间;
的单调区间;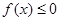 在区间
在区间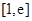 上恒成立,求实数
上恒成立,求实数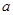 的取值范围.
的取值范围.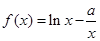 ,
, ,其中
,其中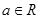 .
. 的单调性;
的单调性;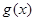 在其定义域内为增函数,求正实数
在其定义域内为增函数,求正实数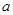 的取值范围;
的取值范围;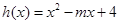 ,当
,当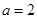 时,若
时,若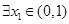 ,
,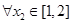 ,总有
,总有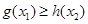 成立,求实数
成立,求实数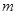 的取值范围.
的取值范围.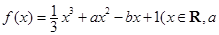 ,
,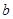 为实数)有极值,且在
为实数)有极值,且在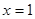 处的切线与直线
处的切线与直线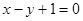 平行.
平行. 的极小值为1,若存在,求出实数a的值;若不存在,请说明理由;
的极小值为1,若存在,求出实数a的值;若不存在,请说明理由;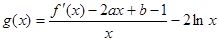 试判断函数
试判断函数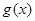 在
在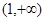 上的符号,并证明:
上的符号,并证明: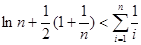 (
(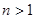 ).
).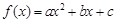 ,
,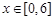 的图象经过
的图象经过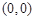 和
和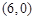 两点,如图所示,且函数
两点,如图所示,且函数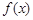 的值域为
的值域为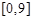 .过该函数图象上的动点
.过该函数图象上的动点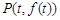 作
作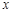 轴的垂线,垂足为
轴的垂线,垂足为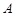 ,连接
,连接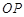 .
.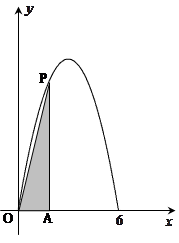
 的面积为
的面积为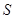 ,求
,求