题目内容
已知函数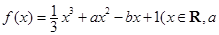 ,
,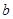 为实数)有极值,且在
为实数)有极值,且在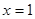 处的切线与直线
处的切线与直线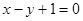 平行.
平行.
(Ⅰ)求实数a的取值范围;
(Ⅱ)是否存在实数a,使得函数 的极小值为1,若存在,求出实数a的值;若不存在,请说明理由;
的极小值为1,若存在,求出实数a的值;若不存在,请说明理由;
(Ⅲ)设函数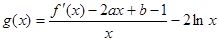 试判断函数
试判断函数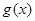 在
在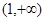 上的符号,并证明:
上的符号,并证明: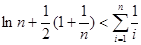 (
(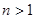 ).
).
(Ⅰ) ;(Ⅱ)
;(Ⅱ)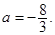 (Ⅲ)见解析.
(Ⅲ)见解析.
解析试题分析:(Ⅰ)由已知在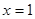 处的切线与直线
处的切线与直线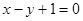 平行,得
平行,得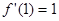 且
且 有两个不等实根,从而得出
有两个不等实根,从而得出 的范围;(Ⅱ)先由导函数得出函数的单调性,确定函数的极小值点,然后由函数
的范围;(Ⅱ)先由导函数得出函数的单调性,确定函数的极小值点,然后由函数 的极小值为1得出存在的
的极小值为1得出存在的 值;(Ⅲ)先确定
值;(Ⅲ)先确定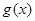 的单调性,
的单调性,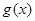 在
在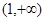 上是增函数,故
上是增函数,故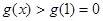 ,构造
,构造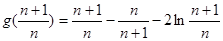
 ,分别取
,分别取 的值为1、2、3、 、
的值为1、2、3、 、 累加即可得证.
累加即可得证.
试题解析:(Ⅰ)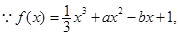
 由题意
由题意
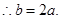 ① (1分)
① (1分)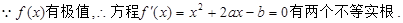
 ②
②
由①、②可得,
故实数a的取值范围是 (3分)
(3分)
(Ⅱ)存在 (5分)
(5分)
由(1)可知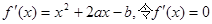 ,
, ,且
,且


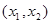
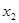
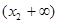
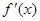
+ 0 - 0 + 
单调增 极大值 单调减 极小值
 练习册系列答案
练习册系列答案
昕金立文化单元金卷系列答案
单元评价测试卷系列答案
学习与评价山东教育出版社系列答案
正大图书中考真题分类卷系列答案
5年中考试卷系列答案
大爱图书纵向解析与命题设计中考试题精选系列答案
首师金卷重点校中考模拟测试卷系列答案
快乐寒假河北少年儿童出版社系列答案
春雨教育考必胜中考试卷精选系列答案
天利38套解锁中考真题档案系列答案
相关题目
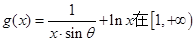 上为增函数,且
上为增函数,且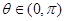 ,
,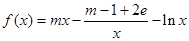 ,
,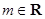 .
.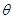 的值;
的值;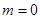 时,求函数
时,求函数 的单调区间和极值;
的单调区间和极值;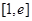 上至少存在一个
上至少存在一个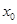 ,使得
,使得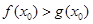 成立,求
成立,求 的取值范围.
的取值范围. ,
, .
. 的单调性;
的单调性; 时,
时, 恒成立,求
恒成立,求 的取值范围.
的取值范围.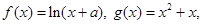 若函数
若函数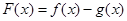 在x = 0处取得极值.
在x = 0处取得极值. 的值;
的值;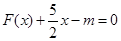 在区间[0,2]上恰有两个不同的实数根,求实数
在区间[0,2]上恰有两个不同的实数根,求实数 的取值范围;
的取值范围;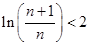 恒成立.
恒成立. ,其中
,其中 是自然对数的底数.
是自然对数的底数. 的单调区间和极值;
的单调区间和极值; 对任意
对任意 满足
满足 ,求证:当
,求证:当 时,
时, ;
; ,且
,且 ,求证:
,求证: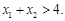
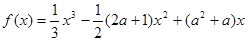 .
.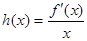 为奇函数,求a的值;
为奇函数,求a的值;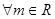 ,直线
,直线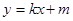 都不是曲线
都不是曲线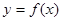 的切线,求k的取值范围;
的切线,求k的取值范围;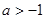 ,求
,求 在区间
在区间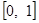 上的最大值.
上的最大值.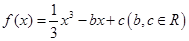
 在点
在点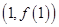 处的切线方程为
处的切线方程为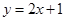 ,求
,求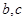 的值;
的值;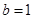 ,函数
,函数 在区间
在区间 内有唯一零点,求
内有唯一零点,求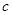 的取值范围;
的取值范围;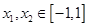 ,均有
,均有 ,求
,求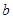 的取值范围.
的取值范围.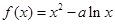 和
和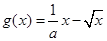 ,且
,且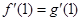 .
. ,
, 的表达式;
的表达式;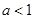 时,不等式
时,不等式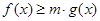 在
在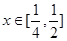 上恒成立,求实数
上恒成立,求实数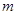 的取值范围.
的取值范围. ,
,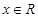 .
.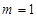 ,
,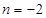 时,求
时,求 的单调区间;
的单调区间;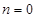 ,且
,且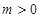 时,求
时,求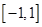 上的最大值.
上的最大值.