题目内容
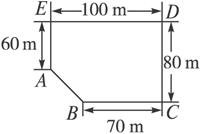
某房地产公司要在荒地ABCDE（如下图）上划出一块长方形土地.（不改变方位）建造一幢8层楼公寓.问如何设计才能使公寓占地面积最大？并求出最大面积（精确到1 m2）.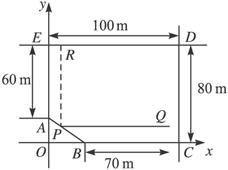
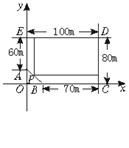
解析：建立坐标系如下图，A（0，20），B（30，0），于是AB的方程为：
=1(0≤x≤30).
在线段EF上取一点P（m，n），作PQ⊥CD于Q.
PR⊥DE于R，设矩形PQDR的面积为S，则：S=|PQ|·|PR|=（100-m）(80-n)
∵
n=20(1-
),
∴S=(100-m)(80-20+
m)=-
(m-5)2+
(0≤x≤30).
于是当m=5时，S有最大值，这时
.
答：当公寓设计成矩形，矩形两边在CD，DE上，一个顶点在线段AB上，且这个顶点分BA成5∶1时，草坪的面积最大.
练习册系列答案
相关题目
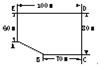某房地产公司要在荒地ABCDE（如图）上划出一块长方形地面（不改变方位）建造一幢八层的公寓楼，问如何设计才能使公寓占地面积最大？并求出最大面积．（精确到1 m2）
某房地产公司要在荒地ABCDE（如图所示）上划出一块长方形地面建造一幢公寓，问：如何设计才能使公寓占地面积最大？求出最大面积（尺寸单位：m）．
m2)．
