题目内容
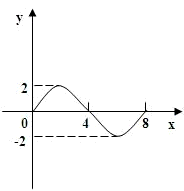
函数f(x)=Asin(ωx+θ)(A>0,ω>0)的部分图象如图所示,则f(1)+f(2)+…+f(2011)的值为
- A.0
- B.2
- C.2+

- D.2+2

D
分析:先根据图象得到最小正周期和θ的值,进而可确定函数f(x)的解析式,然后求出f(1)至f(8)的值,可以得到f(1)+f(2)+…+f(8)=0,最后根据f(1)+f(2)+…+f(2011)=0×251+f(1)+f(2)+f(3)可得到最后答案.
解答:由图可知T=8,
∴w= ,θ=0,
,θ=0,
∴f(x)=sin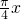
∴f(1)= ,f(2)=2,f(3)=
,f(2)=2,f(3)= ,f(4)=0,f(5)=-
,f(4)=0,f(5)=- ,f(6)=-2,f(7)=-
,f(6)=-2,f(7)=- ,f(8)=0,
,f(8)=0,
f(1)+f(2)+…+f(8)=0
∴f(1)+f(2)+…+f(2011)=0×251+f(1)+f(2)+f(3)=2+2
故选D.
点评:本题主要考查三角函数的最小正周期的求法和解析式的确定.属基础题.
分析:先根据图象得到最小正周期和θ的值,进而可确定函数f(x)的解析式,然后求出f(1)至f(8)的值,可以得到f(1)+f(2)+…+f(8)=0,最后根据f(1)+f(2)+…+f(2011)=0×251+f(1)+f(2)+f(3)可得到最后答案.
解答:由图可知T=8,
∴w=
 ,θ=0,
,θ=0,∴f(x)=sin
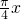
∴f(1)=
 ,f(2)=2,f(3)=
,f(2)=2,f(3)= ,f(4)=0,f(5)=-
,f(4)=0,f(5)=- ,f(6)=-2,f(7)=-
,f(6)=-2,f(7)=- ,f(8)=0,
,f(8)=0,f(1)+f(2)+…+f(8)=0
∴f(1)+f(2)+…+f(2011)=0×251+f(1)+f(2)+f(3)=2+2

故选D.
点评:本题主要考查三角函数的最小正周期的求法和解析式的确定.属基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
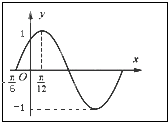 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
 如图所示的是定义域为R的函数f(x)=Asin(ωx+φ)(其中ω>0,φ∈[-π,π))的部分图象,则不等式
如图所示的是定义域为R的函数f(x)=Asin(ωx+φ)(其中ω>0,φ∈[-π,π))的部分图象,则不等式