题目内容
2.设Sn为等差数列{an}的前n项和,S10=110,S15=240.(1)求数列{an}的通项公式;
(2)令bn=$\frac{{{a_{n+1}}}}{a_n}$+$\frac{a_n}{{{a_{n+1}}}}$-2,求数列{bn}的前n项和Tn.
分析 (1)由由等差数列的前n项和公式可知:$\left\{\begin{array}{l}{10{a}_{1}+\frac{10×9}{2}d=110}\\{15{a}_{1}+\frac{15×14}{2}d=240}\end{array}\right.$,即可求得a1和d,即可求得数列{an}的通项公式;
(2)由(1)可知:bn=$\frac{2n+2}{2n}$+$\frac{2n}{2n+2}$=$\frac{n+1}{n}$+$\frac{n}{n+1}$=$\frac{1}{n}$-$\frac{1}{n+1}$+2,采用分组求和,“裂项法”,即可求得数列{bn}的前n项和Tn.
解答 解:(1)设等差数列{an}公差为d,
由等差数列的前n项和公式可知:$\left\{\begin{array}{l}{10{a}_{1}+\frac{10×9}{2}d=110}\\{15{a}_{1}+\frac{15×14}{2}d=240}\end{array}\right.$,整理得:$\left\{\begin{array}{l}{2{a}_{1}+9d=22}\\{{a}_{1}+7d=16}\end{array}\right.$
解得,$\left\{\begin{array}{l}{{a}_{1}=2}\\{d=2}\end{array}\right.$.
由等差数列的通项公式an=2(n-1)+2=2n,
数列{an}的通项公式an=2n;…(6分)
(2)由(1)可知:bn=$\frac{2n+2}{2n}$+$\frac{2n}{2n+2}$=$\frac{n+1}{n}$+$\frac{n}{n+1}$=$\frac{1}{n}$-$\frac{1}{n+1}$+2,
Tn=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{n}$-$\frac{1}{n+1}$+2n,
=$\frac{n}{n+1}$+2n,
=$\frac{2{n}^{2}+3n}{n+1}$,
数列{bn}的前n项和Tn=$\frac{2{n}^{2}+3n}{n+1}$.…(12分)
点评 本题考查等差数列前n项和,考查“裂项法”及分组求和,考查计算能力,属于中档题.

 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案| A. | $\frac{π}{6}$或$\frac{5π}{6}$ | B. | $\frac{π}{4}$或$\frac{5π}{6}$ | C. | $\frac{π}{3}$或$\frac{2π}{3}$ | D. | -$\frac{π}{6}$或-$\frac{5π}{6}$ |
| A. | 8 | B. | 7 | C. | 4 | D. | 3 |
| A. | 公差为9的等差数列 | B. | 公差为$\frac{9}{4}$的等差数列 | ||
| C. | 公差为4 的等差数列 | D. | 不是等差数列 |
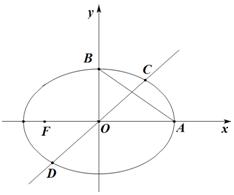 已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,点F、A、B分别为E的左焦点、右顶点,上顶点,|AF|=$\sqrt{2}$+1.
已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,点F、A、B分别为E的左焦点、右顶点,上顶点,|AF|=$\sqrt{2}$+1.