题目内容
点P(x,y)为圆(x-1)2+(y-1)2=1上任意一点,求
的取值范围
| x2+y2 |
[
-1,
+1]
| 2 |
| 2 |
[
-1,
+1]
.| 2 |
| 2 |
分析:(x-1)2+(y-1)2=1表示以(1,1)为圆心,1为半径的圆,
表示(x,y)与原点的距离;
的最大值为圆心到原点的距离加上半径,;最小值为圆心到原点的距离减去半径,由此可确定
的取值范围.
| x2+y2 |
| x2+y2 |
| x2+y2 |
解答:解:(x-1)2+(y-1)2=1表示以(1,1)为圆心,1为半径的圆,
表示(x,y)与原点的距离
∵点P是圆(x-1)2+(y-1)2=1上任意一点
∴
的最大值为圆心到原点的距离加上半径,即
+1;最小值为圆心到原点的距离减去半径,即
-1
故
的取值范围是[
-1,
+1]
故答案为:[
-1,
+1]
| x2+y2 |
∵点P是圆(x-1)2+(y-1)2=1上任意一点
∴
| x2+y2 |
| 2 |
| 2 |
故
| x2+y2 |
| 2 |
| 2 |
故答案为:[
| 2 |
| 2 |
点评:本题考查圆的标准方程,考查两点间的距离,理解
的几何意义是解题的关键.
| x2+y2 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
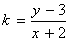 的最大值和最小值。
的最大值和最小值。