题目内容
已知P(x,y)为圆C:x2+y2-4x-14y+45=0上的动点,
(1)求x2+y2+4x-6y+13的最大值和最小值;
(2)求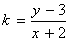 的最大值和最小值。
的最大值和最小值。
(1)求x2+y2+4x-6y+13的最大值和最小值;
(2)求
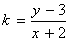 的最大值和最小值。
的最大值和最小值。 解:(1)设Q(-2,3),则x2+y2-4x+6y+13=(x+2)2+(y-3)2=|PQ|2,
∴ |PQ|max=|CQ|+R=6 ,|PQ|min=|CQ|-R=2
,|PQ|min=|CQ|-R=2 ,
,
所以,原式的最大值为72,原式的最小值为8。
(2)依题意,k为(-2,3)与圆C上任意一点连线的斜率,
它的最大值和最小值分别是过(-2,3)的圆C的切线的斜率,
所以,kmax=tan(45°+30°)=2+ ,kmin=tan(45°-30°)=2-
,kmin=tan(45°-30°)=2- ,(注意kQC=1)。
,(注意kQC=1)。
∴ |PQ|max=|CQ|+R=6
 ,|PQ|min=|CQ|-R=2
,|PQ|min=|CQ|-R=2 ,
,所以,原式的最大值为72,原式的最小值为8。
(2)依题意,k为(-2,3)与圆C上任意一点连线的斜率,
它的最大值和最小值分别是过(-2,3)的圆C的切线的斜率,
所以,kmax=tan(45°+30°)=2+
 ,kmin=tan(45°-30°)=2-
,kmin=tan(45°-30°)=2- ,(注意kQC=1)。
,(注意kQC=1)。 
练习册系列答案
相关题目
 在A、B、C、D四小题中只能选做2题,每小题10分,共计20分,请在答题纸指定区域内作答,解答应写出文字说明、证明过程或演算步骤.
在A、B、C、D四小题中只能选做2题,每小题10分,共计20分,请在答题纸指定区域内作答,解答应写出文字说明、证明过程或演算步骤.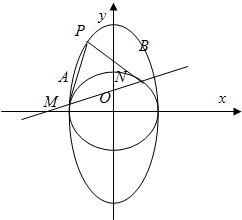 附加题:如图,过椭圆C:
附加题:如图,过椭圆C: (2012•江苏)A.[选修4-1:几何证明选讲]
(2012•江苏)A.[选修4-1:几何证明选讲]