题目内容
20.已知a∈R,(a+cosx)(a-sinx)=1有实根,那么a的范围是[-1-$\frac{\sqrt{2}}{2}$,-1+$\frac{\sqrt{2}}{2}$]∪[1-$\frac{\sqrt{2}}{2}$,1+$\frac{\sqrt{2}}{2}$].分析 若(a+cosx)(a-sinx)=1有实根,则$\frac{1}{2}$(cosx-sinx)2+a(cosx-sinx)+${a}^{2}-\frac{3}{2}$=0有实根,令t=cosx-sinx=$\sqrt{2}$cos(x+$\frac{π}{4}$)∈[-$\sqrt{2}$,$\sqrt{2}$],则方程$\frac{1}{2}$t2+at+${a}^{2}-\frac{3}{2}$=0在[-$\sqrt{2}$,$\sqrt{2}$]上有解,解得a的范围.
解答 解:若(a+cosx)(a-sinx)=1有实根,
则$\frac{1}{2}$(cosx-sinx)2+a(cosx-sinx)+${a}^{2}-\frac{3}{2}$=0有实根,
令t=cosx-sinx=$\sqrt{2}$cos(x+$\frac{π}{4}$)∈[-$\sqrt{2}$,$\sqrt{2}$],
则方程$\frac{1}{2}$t2+at+${a}^{2}-\frac{3}{2}$=0在[-$\sqrt{2}$,$\sqrt{2}$]上有解,
即-a+$\sqrt{3-{a}^{2}}$∈[-$\sqrt{2}$,$\sqrt{2}$],或-a-$\sqrt{3-{a}^{2}}$∈[-$\sqrt{2}$,$\sqrt{2}$],
a∈[-1-$\frac{\sqrt{2}}{2}$,-1+$\frac{\sqrt{2}}{2}$]∪[1-$\frac{\sqrt{2}}{2}$,1+$\frac{\sqrt{2}}{2}$],
故答案为:[-1-$\frac{\sqrt{2}}{2}$,-1+$\frac{\sqrt{2}}{2}$]∪[1-$\frac{\sqrt{2}}{2}$,1+$\frac{\sqrt{2}}{2}$]
点评 本题考查的知识点是函数的零点与方程的根的关系,换元法,不等式的解法,难度中档.

| A. | -12 | B. | -$\frac{1}{12}$ | C. | -$\frac{1}{6}$ | D. | $\frac{1}{16}$ |
| A. | -430 | B. | -470 | C. | 470 | D. | 490 |

| A. | ①③⑤ | B. | ①⑥ | C. | ①③⑥ | D. | ③④⑥ |
 则
则 = .
= .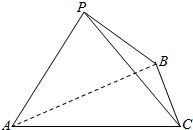 如图,三棱锥P-ABC的底面是边长为2的等边三角形,若$PA=PB=\sqrt{2}$,二面角P-BA-C的大小为60°,则三棱锥P-ABC的外接球的面积等于$\frac{52}{9}π$.
如图,三棱锥P-ABC的底面是边长为2的等边三角形,若$PA=PB=\sqrt{2}$,二面角P-BA-C的大小为60°,则三棱锥P-ABC的外接球的面积等于$\frac{52}{9}π$.