题目内容
观察下列不等式:1+
<
,1+
+
<
,1+
+
+
<
,…由以上不等式推测到一个一般的结论:对于n∈N*,1+
+
+…+
<
.
| 1 |
| 22 |
| 3 |
| 2 |
| 1 |
| 22 |
| 1 |
| 32 |
| 5 |
| 3 |
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| 42 |
| 7 |
| 4 |
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| n2 |
| 2n-1 |
| n |
| 2n-1 |
| n |
分析:由已知中的三个式子,我们分析每一个不等式右边的变化趋势,可以归纳出其通项为
,由此即可得到结论.
| 2n-1 |
| n |
解答:解:由已知中的不等式,1+
<
,1+
+
<
,1+
+
+
<
…
我们可以得出不等式右边分式的分子是正奇数3,5,7,…,分母是正整数2,3,4,…,从而推断:
对于n∈N*,1+
+
+…+
<
.
故答案为:
.
| 1 |
| 22 |
| 3 |
| 2 |
| 1 |
| 22 |
| 1 |
| 32 |
| 5 |
| 3 |
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| 42 |
| 7 |
| 4 |
我们可以得出不等式右边分式的分子是正奇数3,5,7,…,分母是正整数2,3,4,…,从而推断:
对于n∈N*,1+
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| n2 |
| 2n-1 |
| n |
故答案为:
| 2n-1 |
| n |
点评:本题考查的知识点是归纳推理,归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).

练习册系列答案
相关题目
 ,1+
,1+ +
+ >1,1+
>1,1+ +
+ +…+
+…+ >
> ,1+
,1+ +
+ +…+
+…+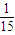 >2,1+
>2,1+ +
+ +…+
+…+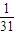 >
> ,…,由此猜测第n个不等式为 (n∈N*).
,…,由此猜测第n个不等式为 (n∈N*).