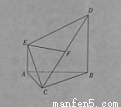
题目内容
如图,在多面体ACBDE中,AE⊥平面ABC,且BD∥AE,AC=AB=BC=BD=2,AE=1,F为CD的中点.(1)求证:EF⊥平面BCD;
(2)求多面体ACBDE的体积.
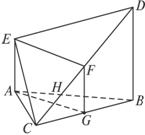
思路分析:(1)直接证EF⊥平面BCD比较困难,注意到中点,考虑将EF平行移动,实现问题的转化;(2)视ACBDE为以ABDE为底的四棱锥.
(1)证明:取BC的中点G,连结FG、AG,则FG=![]() BD=1=AE,且FG∥BD∥AE,
BD=1=AE,且FG∥BD∥AE,
∴AGFE是平行四边形.
∴EF∥AG.在△ABC中,
∵AB=AC,G为BC中点,
∴AG⊥BC.
又∵AE⊥平面ABC,且AG![]() 平面ABC,
平面ABC,
∴AE⊥AG.∴AG⊥FG.
而FG、BC相交,
∴AG⊥平面BCD,从而EF⊥平面BCD.
(2)解:设AB中点为H,因为AC=AB=BC=2,∴CH⊥AB,且CH=![]() .
.
又AE⊥平面ABC,∴平面ABDE⊥平面ABC.
∴CH⊥平面ABDE,于是VC—ABDE=![]() S四边形ABDE=
S四边形ABDE=![]() ·CH.
·CH.

练习册系列答案
相关题目
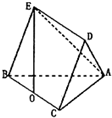 如图,在多面体ABCDE中,底面△ABC为等腰直角三角形,且∠ACB=90°,侧面BCDE是菱形,O点是BC的中点,EO⊥平面ABC.
如图,在多面体ABCDE中,底面△ABC为等腰直角三角形,且∠ACB=90°,侧面BCDE是菱形,O点是BC的中点,EO⊥平面ABC.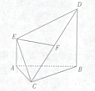 (2012•安徽模拟)如图,在多面体ABCDE中,AE⊥面ABC,DB∥AE,且AC=AB=BC=AE=1,BD=2,F为CD中点.
(2012•安徽模拟)如图,在多面体ABCDE中,AE⊥面ABC,DB∥AE,且AC=AB=BC=AE=1,BD=2,F为CD中点. 如图,在多面体ABCDE中,AE⊥面ABC,DB∥AE,且AC=AB=BC=AE=1,BD=2,F为CD中点.
如图,在多面体ABCDE中,AE⊥面ABC,DB∥AE,且AC=AB=BC=AE=1,BD=2,F为CD中点. (2012•温州二模)如图,在多面体ABCDE中,∠ABC=90°,∠ACB=30°,四边形为等腰梯形,∠EAC=∠DCA=45°,AC=2ED=4,平面BCD丄平面ABE.
(2012•温州二模)如图,在多面体ABCDE中,∠ABC=90°,∠ACB=30°,四边形为等腰梯形,∠EAC=∠DCA=45°,AC=2ED=4,平面BCD丄平面ABE.