题目内容
【题目】设![]() :实数
:实数![]() 满足不等式
满足不等式![]() ,
,![]() :函数
:函数![]() 无极值点.
无极值点.
(1)若“![]() ”为假命题,“
”为假命题,“![]() ”为真命题,求实数
”为真命题,求实数![]() 的取值范围;
的取值范围;
(2)已知“![]() ”为真命题,并记为
”为真命题,并记为![]() ,且
,且![]() :
:![]() ,若
,若![]() 是
是![]() 的必要不充分条件,求正整数
的必要不充分条件,求正整数![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:先将命题化简为![]() :
:![]() ,
, ![]() :
:![]() .(1)易得
.(1)易得![]() 与
与![]() 只有一个命题是真命题.再讨论
只有一个命题是真命题.再讨论![]() 为真命题,
为真命题,![]() 为假命题和
为假命题和![]() 为真命题,
为真命题,![]() 为假命题两种情况;(2)由“
为假命题两种情况;(2)由“![]() ”为真命题
”为真命题![]()
![]() . 又
. 又![]()
![]()
![]() 或
或![]()
![]()
![]() :
:![]() 或
或![]()
![]()
![]() :
:![]() .易得
.易得![]() 是
是![]() 的充分不必要条件
的充分不必要条件![]()

![]()
![]() ,又
,又![]()
![]()
![]() .
.
试题解析:解:由![]() ,得
,得![]() ,即
,即![]() :
:![]() .
.
∵函数![]() 无极值点,∴
无极值点,∴![]() 恒成立,得
恒成立,得![]() ,解得
,解得![]() ,
,
即![]() :
:![]() .
.
(1)∵“![]() ”为假命题,“
”为假命题,“![]() ”为真命题,∴
”为真命题,∴![]() 与
与![]() 只有一个命题是真命题.
只有一个命题是真命题.
若![]() 为真命题,
为真命题,![]() 为假命题,则
为假命题,则![]() .
.
若![]() 为真命题,
为真命题,![]() 为假命题,则
为假命题,则![]() .
.
于是,实数![]() 的取值范围为
的取值范围为![]() .
.
(2)∵“![]() ”为真命题,∴
”为真命题,∴![]() .
.
又![]() ,
,
∴![]() ,
,
∴![]() 或
或![]() ,
,
即![]() :
:![]() 或
或![]() ,从而
,从而![]() :
:![]() .
.
∵![]() 是
是![]() 的必要不充分条件,即
的必要不充分条件,即![]() 是
是![]() 的充分不必要条件,
的充分不必要条件,
∴ ,解得
,解得![]() ,∵
,∵![]() ,∴
,∴![]()

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
【题目】某同学的父亲决定今年夏天卖西瓜赚钱,根据去年6月份的数据统计连续五天内每天所卖西瓜的个数与温度之间的关系如下表:
温度 | 32 | 33 | 35 | 37 | 38 |
西瓜个数 | 20 | 22 | 24 | 30 | 34 |
(1)求这五天内所卖西瓜个数的平均值和方差;
(2)求变量![]() 之间的线性回归方程,并预测当温度为
之间的线性回归方程,并预测当温度为![]() 时所卖西瓜的个数.
时所卖西瓜的个数.
附: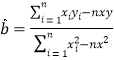 ,
,![]() (精确到
(精确到![]() ).
).