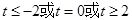题目内容
若函数 上不是单调函数,则函数
上不是单调函数,则函数 在区间
在区间 上的图象可能是 ( )
上的图象可能是 ( )
| A.①③ | B.②④ | C.②③ | D.③④ |
D
解析试题分析:根据函数的增长快慢与导数值的关系,对图象逐一分析可得答案.解:①中函数增长的越来越快说明函数的导数值越来越大,故导函数单调增,②中函数增长的越来越慢说明函数的导数值越来越小,故导函数单调减,③中函数增长相同,导数值等于常数,无单调性,④中函数增长的先快后慢,说明导数值先大后小,故导函数不是单调函数,故选D.
考点:函数图像
点评:本题主要考查函数的增加快慢和导数值的变化之间的关系.属基础题

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
函数 在
在 上的最大值和最小值分别是( )
上的最大值和最小值分别是( )
| A.2,1 | B.2,-7 | C.2,-1 | D.-1,-7 |
下列说法中,不正确的是
A.点 为函数 为函数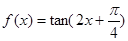 的一个对称中心 的一个对称中心 |
B.设回归直线方程为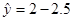 x,当变量x增加一个单位时,y大约减少2.5个单位 x,当变量x增加一个单位时,y大约减少2.5个单位 |
| C.命题“在△ABC中,若sinA="sin" B,则△ABC为等腰三角形”的逆否命题为真命题 |
D.对于命题p:“ ”则 ”则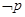 “ “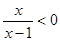 ” ” |
已知定义在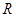 上的函数
上的函数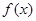 ,对任意的
,对任意的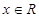 ,都有
,都有 成立,若函数
成立,若函数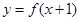 的图象关于直线
的图象关于直线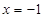 对称,则
对称,则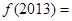
A. | B.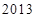 | C. | D.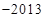 |
函数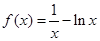 的零点个数为( )
的零点个数为( )
A. | B. | C.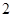 | D.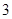 |
已知函数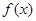 是定义在
是定义在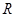 上的奇函数,且满足
上的奇函数,且满足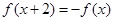 ,当
,当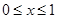 时,
时,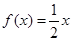 ,则满足
,则满足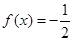 的
的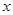 的值是( )
的值是( )
A.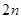 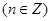 | B.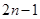 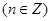 |
C.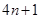 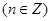 | D.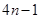 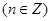 |
函数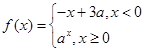
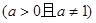 是R上的减函数,则a的取值范围是( )
是R上的减函数,则a的取值范围是( )
| A.(0,1) | B.[ 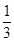 ,1) ,1) | C.(0,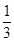 ] ] | D.( 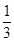 ,1) ,1) |
已知下列不等式: ,则在
,则在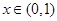 内上述不等式恒成立的个数为( )
内上述不等式恒成立的个数为( )
| A.1 | B.2 | C.3 | D.4 |
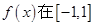 上是增函数,且
上是增函数,且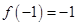 ,若函数
,若函数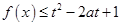 对所有的
对所有的 都成立,则当
都成立,则当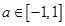 时t的取值范围是 ( )
时t的取值范围是 ( )