题目内容
函数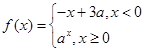
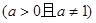 是R上的减函数,则a的取值范围是( )
是R上的减函数,则a的取值范围是( )
| A.(0,1) | B.[ 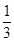 ,1) ,1) | C.(0,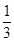 ] ] | D.( 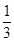 ,1) ,1) |
B
解析试题分析:∵函数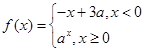
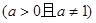 是R上的减函数,∴
是R上的减函数,∴ ,∴
,∴ ,故选B
,故选B
考点:本题考查了函数的单调性
点评:解决此类问题要注意分段函数的单调性与各段函数的单调性的联系与区别

练习册系列答案
相关题目
设函数 是定义在
是定义在 上的奇函数,且对任意
上的奇函数,且对任意 都有
都有 ,当
,当  时,
时, ,则
,则 的值为( )
的值为( )
A. | B. | C.2 | D. |
函数 的递增区间是( )
的递增区间是( )
A. | B. | C. | D. |
若函数 上不是单调函数,则函数
上不是单调函数,则函数 在区间
在区间 上的图象可能是 ( )
上的图象可能是 ( )
| A.①③ | B.②④ | C.②③ | D.③④ |
函数 与
与 在区间[1,2]上都是减函数,则a的取值范围是
在区间[1,2]上都是减函数,则a的取值范围是
A. | B. |
C. | D. |
若函数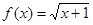 ,则
,则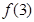 = ( )
= ( )
| A.2 | B.4 | C. | D.0 |
已知函数y=f(x)在(0,2)上是增函数,函数f(x+2)是偶函数,则
A. | B. |
C. | D. |
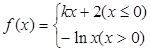 ,则下列关于
,则下列关于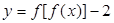 的零点个数判断正确的是( )
的零点个数判断正确的是( )
| A.当k=0时,有无数个零点 | B.当k<0时,有3个零点 |
| C.当k>0时,有3个零点 | D.无论k取何值,都有4个零点 |
已知函数 的值域为
的值域为 ,函数
,函数 的定义域为
的定义域为 ,则
,则
A. | B. | C. | D. |