题目内容
7.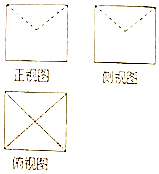 某几何体的三视图如图所示,图中的四边形都是边长为1的正方体,两条虚线互相垂直,则该几何体的体积是( )
某几何体的三视图如图所示,图中的四边形都是边长为1的正方体,两条虚线互相垂直,则该几何体的体积是( )| A. | $\frac{2}{3}$ | B. | $\frac{5}{6}$ | C. | $1-\frac{π}{6}$ | D. | $1-\frac{π}{3}$ |
分析 由已知中的三视图,可得该几何体是一个正方体切去一个正四棱锥所得的组合体,进而得到答案.
解答 解:由已知中的三视图,可得该几何体是一个正方体切去一个正四棱锥所得的组合体,
正方体的棱长为1,故体积为1,
正四棱锥的底面面积为1,高为$\frac{1}{2}$,故体积为:$\frac{1}{3}×\frac{1}{2}×1$=$\frac{1}{6}$,
故组合体的体积V=1-$\frac{1}{6}$=$\frac{5}{6}$.
故选:B.
点评 本题考查的知识点是棱柱的体积和表面积,棱锥的体积和表面积,简单几何体的三视图,难度中档.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
17.设函数f(x)是定义在R上的函数,满足f(x)=f(4-x),且对任意x1,x2∈(0,+∞),都有(x1-x2)[f(x1+2)-f(x2+2)]>0,则满足f(2-x)=f($\frac{3x+11}{x+4}$)的所有x的和为( )
| A. | -3 | B. | -5 | C. | -8 | D. | 8 |
18.一个棱长为6的正四面体纸盒内放一个正方体,若正方体可以在纸盒内任意转动,则正方体棱长的最大值为( )
| A. | 3 | B. | 2 | C. | $\sqrt{2}$ | D. | 1 |
2.执行如图所示的程序框图,则输出的a值为( )
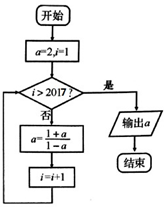

| A. | -3 | B. | $\frac{1}{3}$ | C. | $-\frac{1}{2}$ | D. | 2 |
12.定义在R上的偶函数f(x)的导函数为f'(x),若对任意的实数x,都有2f(x)+xf'(x)<2恒成立,则使x2f(x)-4f(2)<x2-4成立的实数x的取值范围是( )
| A. | (-∞,-2)∪(2,+∞) | B. | (-2,0)∪(0,2) | C. | {x|x≠±2} | D. | (-2,2) |
19.以(1,0),(-1,0)为焦点的椭圆与y=x-2有公共点,则该椭圆离心率的最大值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{10}}}{5}$ |
17.已知双曲线$\frac{x^2}{m}-{y^2}=1$的一个顶点坐标为(2,0),则此双曲线的渐近线方程为( )
| A. | $y=±\frac{{\sqrt{2}}}{2}x$ | B. | $y=±\sqrt{2}x$ | C. | y=±2x | D. | $y=±\frac{1}{2}x$ |
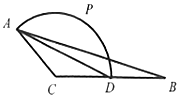 已知△ABC中,AC=2,BC=4,AB=2$\sqrt{7}$,且D是BC的中点.
已知△ABC中,AC=2,BC=4,AB=2$\sqrt{7}$,且D是BC的中点.