题目内容
设斜率为1的直线l与椭圆C: +
+ =1相交于不同的两点A、B,则使|AB|为整数的直线l共有( )
=1相交于不同的两点A、B,则使|AB|为整数的直线l共有( )A.4条
B.5条
C.6条
D.7条
【答案】分析:设直线AB的方程代入椭圆方程,根据判别式求得b的范围,设A(x1,y1),B(x2,y2)则可表示出|AB|,根据|AB|为整数求得b,进而求得答案.
解答:解:设直线AB的方程为y=x+b,代入椭圆C: +
+ =1,
=1,
可得3x2+4bx+2b2-4=0,
由△=16b2-12(2b2-4)>0,可得b2<6,
设A(x1,y1),B(x2,y2),
则|AB|= ×
× =
= ×
× =
=
 ,
,
分别取b2= ,
, ,
, 时,
时,
可分别得|AB|=2,1,3,
此时对应的直线l有6条.
故选C
点评:本题主要考查了直线与圆锥曲线的综合问题.解题的关键找到直线与|AB|的相关性,以此建立等式.
解答:解:设直线AB的方程为y=x+b,代入椭圆C:
 +
+ =1,
=1,可得3x2+4bx+2b2-4=0,
由△=16b2-12(2b2-4)>0,可得b2<6,
设A(x1,y1),B(x2,y2),
则|AB|=
 ×
× =
= ×
× =
=
 ,
,分别取b2=
 ,
, ,
, 时,
时,可分别得|AB|=2,1,3,
此时对应的直线l有6条.
故选C
点评:本题主要考查了直线与圆锥曲线的综合问题.解题的关键找到直线与|AB|的相关性,以此建立等式.

练习册系列答案
相关题目
设斜率为1的直线l与椭圆C:
+
=1相交于不同的两点A、B,则使|AB|为整数的直线l共有( )
| x2 |
| 4 |
| y2 |
| 2 |
| A、4条 | B、5条 | C、6条 | D、7条 |
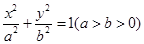 的离心率为
的离心率为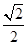 ,且经过点
,且经过点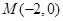 .
. ,
,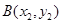 两点,连接MA,MB并延长交直线x=4于P,Q两点,设yP,yQ分别为点P,Q的纵坐标,且
两点,连接MA,MB并延长交直线x=4于P,Q两点,设yP,yQ分别为点P,Q的纵坐标,且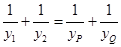 .求△ABM的面积.
.求△ABM的面积.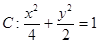 相交于不同的两点A、B,则使|AB|为整数的直线l共有
相交于不同的两点A、B,则使|AB|为整数的直线l共有