题目内容
已知椭圆C: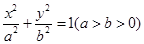 的离心率为
的离心率为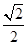 ,且经过点
,且经过点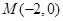 .
.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)设斜率为1的直线l与椭圆C相交于 ,
,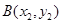 两点,连接MA,MB并延长交直线x=4于P,Q两点,设yP,yQ分别为点P,Q的纵坐标,且
两点,连接MA,MB并延长交直线x=4于P,Q两点,设yP,yQ分别为点P,Q的纵坐标,且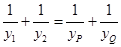 .求△ABM的面积.
.求△ABM的面积.
【答案】
(1) (2)
(2) .
.
【解析】
试题分析:解:(Ⅰ)依题意 ,
, ,所以
,所以 . 2分
. 2分
因为 , 所以
, 所以 . 3分
. 3分
椭圆方程为 . 5分
. 5分
(Ⅱ)因为直线l的斜率为1,可设l: , 6分
, 6分
则 ,
,
消y得  , 7分
, 7分
 ,得
,得 .
.
因为 ,
, ,
,
所以  ,
, . 8分
. 8分
设直线MA: ,则
,则 ;同理
;同理 .
9分
.
9分
因为  ,
,
所以  , 即
, 即 . 10分
. 10分
所以  ,
,
所以  ,
,
 ,
,
 ,
,
所以  , 所以
, 所以
 . 12分
. 12分
所以  ,
, .
.
设△ABM的面积为S,直线l与x轴交点记为N,
所以 .
.
所以 △ABM的面积为 . 14分
. 14分
考点:直线与椭圆的位置关系
点评:主要是考查了直线与椭圆的位置关系以及韦达定理的运用,属于中档题。

练习册系列答案
相关题目
 的离心率为
的离心率为 ,且经过点
,且经过点 .
.
 的离心率为
的离心率为 ,过右焦点
,过右焦点 且斜率为
且斜率为 的直线与椭圆C相交于
的直线与椭圆C相交于 、
、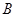 两点.若
两点.若 ,则
,则 =( )
=( )  B.
B. C.2
D.
C.2
D.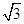
 ,它的离心率为
,它的离心率为 .直线
.直线 与以原点为圆心,以C的短半轴为半径的圆O相切. 求椭圆C的方程.
与以原点为圆心,以C的短半轴为半径的圆O相切. 求椭圆C的方程. 的离心率为
的离心率为 ,椭圆C上任意一点到椭圆两个焦点的距离之和为6.
,椭圆C上任意一点到椭圆两个焦点的距离之和为6. :
: 与椭圆C交于
与椭圆C交于 ,
, 两点,点
两点,点 ,且
,且 ,求直线
,求直线