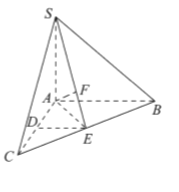
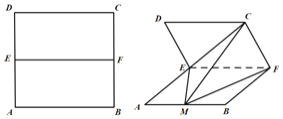
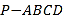ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΥφΉ≈÷«Ρή ÷ΜζΒΡΤ’ΦΑΘ§ Ι”Ο ÷Μζ…œΆχ≥…ΈΣΝΥ»ΥΟ«»’≥Θ…ζΜνΒΡ“Μ≤ΩΖ÷Θ§ΚήΕύœϊΖ―’ΏΕ‘ ÷ΜζΝςΝΩΒΡ–η«σ‘Ϋά¥‘Ϋ¥σ.≥Λ…≥Ρ≥Ά®–≈ΙΪΥΨΈΣΝΥΗϋΚΟΒΊ¬ζΉψœϊΖ―’ΏΕ‘ΝςΝΩΒΡ–η«σΘ§ΉΦ±ΗΆΤ≥ω“ΜΩνΝςΝΩΑϋ.ΗΟΆ®–≈ΙΪΥΨ―ΓΝΥ5Ηω≥« –Θ®Ήή»Υ ΐΓΔΨ≠ΦΟΖΔ’Ι«ιΩωΓΔœϊΖ―ΡήΝΠΒ»ΖΫΟφ±»ΫœΫ”ΫϋΘ©≤…”Ο≤ΜΆ§ΒΡΕ®ΦέΖΫΑΗΉςΈΣ ‘ΒψΘ§Ψ≠Ιΐ“ΜΗω‘¬ΒΡΆ≥ΦΤΘ§ΖΔœ÷ΗΟΝςΝΩΑϋΒΡΕ®Φέ![]() :(ΒΞΈΜΘΚ‘Σ/‘¬Θ©ΚΆΙΚ¬ρ»Υ ΐ
:(ΒΞΈΜΘΚ‘Σ/‘¬Θ©ΚΆΙΚ¬ρ»Υ ΐ![]() (ΒΞΈΜΘΚΆρ»ΥΘ©ΒΡΙΊœΒ»γ±μ:
(ΒΞΈΜΘΚΆρ»ΥΘ©ΒΡΙΊœΒ»γ±μ:
![]()
Θ®1Θ©ΗυΨί±μ÷–ΒΡ ΐΨίΘ§‘Υ”ΟœύΙΊœΒ ΐΫχ––Ζ÷ΈωΥΒΟςΘ§ «ΖώΩ…“‘”ΟœΏ–‘ΜΊΙιΡΘ–ΆΡβΚœ![]() ”κ
”κ![]() ΒΡΙΊœΒΘΩ≤Δ÷Η≥ω «’ΐœύΙΊΜΙ «ΗΚœύΙΊΘΜ
ΒΡΙΊœΒΘΩ≤Δ÷Η≥ω «’ΐœύΙΊΜΙ «ΗΚœύΙΊΘΜ
Θ®2Θ©ΔΌ«σ≥ω![]() ΙΊ”Ύ
ΙΊ”Ύ![]() ΒΡΜΊΙιΖΫ≥ΧΘΜ
ΒΡΜΊΙιΖΫ≥ΧΘΜ
ΔΎ»τΗΟΆ®–≈ΙΪΥΨ‘Ύ“ΜΗωάύΥΤ”Ύ ‘ΒψΒΡ≥« –÷–ΫΪ’βΩνΝςΝΩΑϋΒΡΦέΗώΕ®ΈΜ25‘Σ/ ‘¬Θ§«κ”ΟΥυ«σΜΊΙιΖΫ≥Χ‘Λ≤β≥Λ…≥ –“ΜΗω‘¬ΡΎΙΚ¬ρΗΟΝςΝΩΑϋΒΡ»Υ ΐΡήΖώ≥§Ιΐ20 Άρ»Υ.
≤ΈΩΦ ΐΨίΘΚ![]() Θ§
Θ§![]() Θ§
Θ§![]() .
.
≤ΈΩΦΙΪ ΫΘΚœύΙΊœΒ ΐ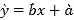 Θ§ΜΊΙι÷±œΏΖΫ≥Χ
Θ§ΜΊΙι÷±œΏΖΫ≥Χ![]() Θ§
Θ§
Τδ÷–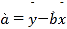 Θ§
Θ§![]() .
.
ΓΨ¥πΑΗΓΩ(1)ΦϊΫβΈω;(2)ΔΌ![]() ;ΔΎ“ΜΗω‘¬ΡΎΙΚ¬ρΗΟΝςΝΩΑϋΒΡ»Υ ΐΜα≥§Ιΐ20Άρ»Υ.
;ΔΎ“ΜΗω‘¬ΡΎΙΚ¬ρΗΟΝςΝΩΑϋΒΡ»Υ ΐΜα≥§Ιΐ20Άρ»Υ.
ΓΨΫβΈωΓΩ
(1) ΗυΨίΧβ“βΘ§ΒΟ![]() ,
,![]() ΦΤΥψ≥ωœύΙΊœΒ ΐ
ΦΤΥψ≥ωœύΙΊœΒ ΐ![]() Θ§¥”ΕχΩ…“‘Ής≥ω≈–Εœ;
Θ§¥”ΕχΩ…“‘Ής≥ω≈–Εœ;
(2) ΔΌ«σ≥ωΜΊΙι÷±œΏΖΫ≥ΧΘ§ΔΎ”…ΔΌ÷ΣΘ§»τ![]() Θ§‘ρ
Θ§‘ρ![]() Θ§¥”Εχ‘Λ≤β≥Λ…≥ –“ΜΗω‘¬ΡΎΙΚ¬ρΗΟΝςΝΩΑϋΒΡ»Υ ΐΜα≥§Ιΐ20Άρ»Υ
Θ§¥”Εχ‘Λ≤β≥Λ…≥ –“ΜΗω‘¬ΡΎΙΚ¬ρΗΟΝςΝΩΑϋΒΡ»Υ ΐΜα≥§Ιΐ20Άρ»Υ
Θ®1Θ©ΗυΨίΧβ“βΘ§ΒΟ![]() Θ§
Θ§
![]() .
.
Ω…Ν–±μ»γœ¬
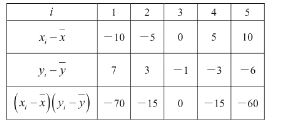
ΗυΨί±μΗώΚΆ≤ΈΩΦ ΐΨίΘ§ΒΟ![]() Θ§
Θ§
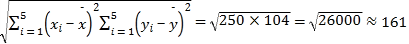 .
.
“ρΕχœύΙΊœΒ ΐ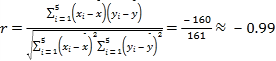 .
.
”…”Ύ![]() ΚήΫ”Ϋϋ1Θ§“ρΕχΩ…“‘”ΟœΏ–‘ΜΊΙιΖΫ≥ΧΡΘ–ΆΡβΚœ
ΚήΫ”Ϋϋ1Θ§“ρΕχΩ…“‘”ΟœΏ–‘ΜΊΙιΖΫ≥ΧΡΘ–ΆΡβΚœ![]() ”κ
”κ![]() ΒΡΙΊœΒ.
ΒΡΙΊœΒ.
”…”Ύ![]() Θ§Ι ΤδΙΊœΒΈΣΗΚœύΙΊ.
Θ§Ι ΤδΙΊœΒΈΣΗΚœύΙΊ.
Θ®2Θ©ΔΌ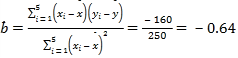 Θ§
Θ§![]() Θ§
Θ§
“ρΕχ![]() ΙΊ”Ύ
ΙΊ”Ύ![]() ΒΡΜΊΙιΖΫ≥ΧΈΣ
ΒΡΜΊΙιΖΫ≥ΧΈΣ![]() .
.
ΔΎ”…ΔΌ÷ΣΘ§»τ![]() Θ§‘ρ
Θ§‘ρ![]() Θ§Ι »τΫΪΝςΝΩΑϋΒΡΦέΗώΕ®ΈΣ25‘Σ/‘¬Θ§Ω…‘Λ≤β≥Λ…≥ –“ΜΗω‘¬ΡΎΙΚ¬ρΗΟΝςΝΩΑϋΒΡ»Υ ΐΜα≥§Ιΐ20Άρ»Υ.
Θ§Ι »τΫΪΝςΝΩΑϋΒΡΦέΗώΕ®ΈΣ25‘Σ/‘¬Θ§Ω…‘Λ≤β≥Λ…≥ –“ΜΗω‘¬ΡΎΙΚ¬ρΗΟΝςΝΩΑϋΒΡ»Υ ΐΜα≥§Ιΐ20Άρ»Υ.

 ΧλΧλœρ…œ“Μ±ΨΚΟΨμœΒΝ–¥πΑΗ
ΧλΧλœρ…œ“Μ±ΨΚΟΨμœΒΝ–¥πΑΗ –Γ―ß…ζ10Ζ÷÷””Π”ΟΧβœΒΝ–¥πΑΗ
–Γ―ß…ζ10Ζ÷÷””Π”ΟΧβœΒΝ–¥πΑΗΓΨΧβΡΩΓΩΟάΙζ÷Τ≤Ο÷––ΥΘ§Έ¥ά¥7Ρξ“ΜΩ≈–ΨΤ§ΕΦ≤Μ¬τΘ§’⻥ΦΛΖΔΝΥ÷–ΙζΓΑ–ΨΓ±ΒΡ―–ΨΩ»»≥±.Ρ≥ΙΪΥΨΦΉΘ§““Θ§±ϊ»ΐΗω―–ΖΔ–ΓΉιΖ÷±π―–ΖΔ![]() Θ§
Θ§![]() Θ§
Θ§![]() »ΐ÷÷≤ΜΆ§ΒΡ–ΨΤ§Θ§œ÷‘Ύ”ΟΖ÷≤ψ≥ι―υΒΡΖΫΖ®¥”’β–©–ΨΤ§÷–≥ι»Γ»τΗ…ΦΰΫχ––÷ ΝΩΖ÷ΈωΘ§”–ΙΊ ΐΨίΦϊœ¬±μΘ®ΒΞΈΜΘΚΦΰΘ©.
»ΐ÷÷≤ΜΆ§ΒΡ–ΨΤ§Θ§œ÷‘Ύ”ΟΖ÷≤ψ≥ι―υΒΡΖΫΖ®¥”’β–©–ΨΤ§÷–≥ι»Γ»τΗ…ΦΰΫχ––÷ ΝΩΖ÷ΈωΘ§”–ΙΊ ΐΨίΦϊœ¬±μΘ®ΒΞΈΜΘΚΦΰΘ©.
–ΨΤ§ | ΐΝΩ | ≥ι»ΓΦΰ ΐ |
| 200 |
|
| 600 |
|
| 400 | 2 |
Θ®ΔώΘ©«σ![]() ΒΡ÷ΒΘΜ
ΒΡ÷ΒΘΜ
Θ®ΔρΘ©»τ‘Ύ’β≥ι≥ωΒΡ―υΤΖ÷–ΥφΜζ≥ι»Γ2ΦΰΥΆΆυΡ≥ΜζΙΙΫχ––Ϋχ“Μ≤ΫΦλ≤βΘ§«σ’β2Φΰ–ΨΤ§ά¥Ή‘≤ΜΆ§÷÷άύΒΡΗ≈¬ .