Question

【题目】已知正方形的边长为4，，分别为，的中点，以为棱将正方形折成如图所示的的二面角，点在线段上且不与点，重合，直线与由，，三点所确定的平面相交，交点为．

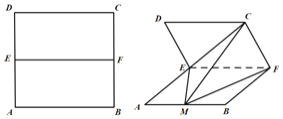
（1）若为的中点，试确定点的位置，并证明直线平面；

（2）若，求的长度，并求此时点到平面的距离．

Answer 1

【答案】（1）见解析；（2）

【解析】

（1）延长交的延长线于，连接交于，利用平面几何知识得，再根据线面平行判定定理得结论，（2）根据线线垂直、线面垂直关系将条件转化到平面内垂直关系，再根据相似三角形以及直角三角形计算得结果．

(1)延长交的延长线于，

为中点，，为中点，

又，为中点，

连接交于，则为中点，所以，

又平面，平面，平面；

（2）由题意可知，所以平面，同理可得平面，因为二面角为60°, ，与是全等的正三角形，取中点，则,由平面，平面得,因此平面，即,平面，

设，

的长度为．

过作于,则由平面，得平面，即为点到平面的距离，

点到平面的距离为．