题目内容
已知二次函数f(x)满足f(x+1)-f(x)=2x,且f(0)=1.
(1)求解析式f(x);
(2)当x∈[-1, 1]时,函数y=f(x)的图象恒在函数y=2x+m的图象的上方,求实数m的取值范围。
解:(1)已知函数f(x)=ax2+bx+c
由f(0)=1可知c=1
由f(x+1)-f(x)=2ax+a+b=2x
则 ,∴
,∴ ,∴f(x)=x2-x+1
,∴f(x)=x2-x+1
(2)即f(x)>2x+m在x∈[-1, 1]上恒成立
X2-x+1>2x+m
∴m<(x2-3x+1)min,
而x2-3x+1=(x― )2―
)2― 在[―1, 1]上递减
在[―1, 1]上递减
∴m<-1

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
某产品的广告费用与销售额的统计数据如下表:
| 广告费用x(万元) | 4 | 2 | 3 | 5 |
| 销售额y(万元) | 49 | 26 | 39 | 54 |
根据上表可得回归方程y=bx+a中的b为9.4,据此模型预报广告费用为6万元时销售额为( )
A.63.6万元 B.65.5万元 C. 67.7万元 D.72.0万元
 )
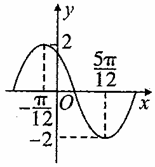
)
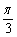 )
)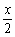 -
- ”是“α=
”是“α= ”的充分不必要条件
”的充分不必要条件 ≤0”
≤0”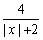 -1的定义域是[a, b](a, b∈Z),值域是[0, 1],则满足条件的整数对(a, b)共有
-1的定义域是[a, b](a, b∈Z),值域是[0, 1],则满足条件的整数对(a, b)共有