Question

12．设F₁、F₂分别是椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$的左、右焦点，过原点的直线交椭圆于A、B两点，AF₂⊥BF₂，|AF₂|=6，|BF₂|=8，则椭圆C的方程为$\frac{{x}^{2}}{49}+\frac{{y}^{2}}{24}$=1．

Answer 1

分析 如图所示，由椭圆的对称性可得：OA=OB，又F₁O=F₂O，及其AF₂⊥BF₂，可得四边形AF₁BF₂是矩形，再利用椭圆的定义及其勾股定理即可得出．

解答 解：如图所示，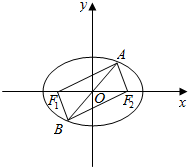
由椭圆的对称性可得：OA=OB，
又F₁O=F₂O，
∴四边形AF₁BF₂是平行四边形，
又AF₂⊥BF₂，
∴四边形AF₁BF₂是矩形，
∵|AF₂|=6，|BF₂|=8，
∴|F₁F₂|=$\sqrt{{6}^{2}+{8}^{2}}$=10=2c，2a=6+8，
解得c=5，a=7．
∴b²=a²-c²=24．
∴椭圆C的方程为$\frac{{x}^{2}}{49}+\frac{{y}^{2}}{24}$=1．
故答案为：$\frac{{x}^{2}}{49}+\frac{{y}^{2}}{24}$=1．

点评 本题考查了椭圆的定义标准方程及其性质、平行四边形与矩形的定义与性质、勾股定理，考查了推理能力与计算能力，属于中档题．