题目内容
20.某市区甲、乙、丙三所学校的高三文科学生共有800人,其中男、女生人数如表:| 甲校 | 乙校 | 丙校 | |
| 男生 | 97 | 90 | x |
| 女生 | 153 | y | z |
(1)求表中x+z的值;
(2)某市四月份模考后,市教研室准备从这三所学校的所有高三文科学生中利用随机数表法抽取100人进行成绩统计分析.先将800人按001,002,…,800进行编号.如果从第8行第7列的数开始向右读,请你依次写出最先检测的4个人的编号:(下面摘取了随机数表中第7行至第9行)
| 8442 | 1753 | 3157 | 2455 | 0688 | 7704 | 7447 | 6721 | 7633 | 5026 | 8392 |
| 6301 | 5316 | 5916 | 9275 | 3862 | 9821 | 5071 | 7512 | 8673 | 5807 | 4439 |
| 1326 | 3321 | 1342 | 7864 | 1607 | 8252 | 0744 | 3815 | 0324 | 4299 | 7931 |
分析 (1)利用在三所高中的所有高三文科学生中随机抽取1人,抽到乙高中女生的概率为0.2,求出表中y的值,再很据总数,求的x+z的值;
(2)根据从第8行第7列的数开始向右读,即可写出最先检测的4个人的编号;
(3)“丙校高三文科生中的男生比女生人数多”为事件A,其中男女生数即为(x,z),一一列举所有的基本事件,根据概率公式计算即可
解答 解:(1)∵在所有高三文科学生中随机抽取1人,抽到乙高中女生的概率为0.2,
∴y=800×0.2=160,则x+z=800-(97+153+90+160)=300,…(4分)
(2)最先检测的4个人的编号为165、538、707、175;…(8分)
(3)设:“丙校高三文科生中的男生比女生人数多”为事件A,其中男女生数即为(x,z)
由(1)知,x+z=300,x≥145,z≥145,
满足条件的(x,z)有(145,155),(146,154),(147,153),(148,152),(149,131),(150,150),(151,149),(152,148),(153,147),(154,146),(155,145)共11组,且每组出现的可能性相同,其中事件A包含的基本事件有:
(151,149),(152,148),(153,147),(154,146),(155,145),共5组,
∴丙高中学校中的女生比男生人数多的概率为P(A)=$\frac{5}{11}$.…(12分)
点评 本题考查概率的应用,考查学生分析解决问题的能力,正确计算是关键.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
11.过点A(3,1)的直线l与圆C:x2+y2-4y-1=0相切于点B,则$\overrightarrow{CA}•\overrightarrow{CB}$=( )
| A. | 0 | B. | $\sqrt{5}$ | C. | 5 | D. | $\frac{{\sqrt{50}}}{3}$ |
8.复数Z=$\frac{2+ai}{1+i}$(a∈R)在复平面内对应的点在虚轴上,则a=( )
| A. | 2 | B. | -2 | C. | 1 | D. | -1 |
15.若复数$\frac{a-3i}{1-2i}$(a∈R,i为虚数单位)是纯虚数,则实数a的值为( )
| A. | -2 | B. | 4 | C. | -6 | D. | 6 |
12.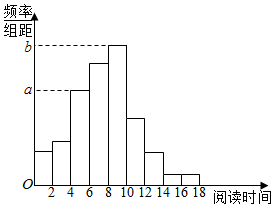 从某校随机抽取200名学生,获得了他们的一周课外阅读时间(单位:小时)的数据,整理得到数据分组级频数分布直方图:
从某校随机抽取200名学生,获得了他们的一周课外阅读时间(单位:小时)的数据,整理得到数据分组级频数分布直方图:
(1)从该校随机选取一名学生,试估计这名学生该周课外阅读时间少于12小时的概率;
(2)求频率分布直方图中的a,b的值;
(3)假设同一组中的每个数据可用该组区间的中点值代替,试估计样本中的200名学生该周课外阅读时间的平均数在第几组.
 从某校随机抽取200名学生,获得了他们的一周课外阅读时间(单位:小时)的数据,整理得到数据分组级频数分布直方图:
从某校随机抽取200名学生,获得了他们的一周课外阅读时间(单位:小时)的数据,整理得到数据分组级频数分布直方图:| 编号 | 分组 | 频数 |
| 1 | [0,2) | 12 |
| 2 | [2,4) | 16 |
| 3 | [4,6) | 34 |
| 4 | [6,8) | 44 |
| 5 | [8,10) | 50 |
| 6 | [10,12) | 24 |
| 7 | [12,14) | 12 |
| 8 | [14,16) | 4 |
| 9 | [16,18) | 4 |
| 合计 | 200 | |
(2)求频率分布直方图中的a,b的值;
(3)假设同一组中的每个数据可用该组区间的中点值代替,试估计样本中的200名学生该周课外阅读时间的平均数在第几组.