题目内容
3.抛物线y2=ax(a>0)与直线x=1围成的封闭图形的面积为$\frac{4}{3}$,则二项式(x+$\frac{a}{x}$)20展开式中含x-16项的系数是190.分析 利用定积分,列出关于面积的式子,求出a,再利用二项式定理求系数的方法求解.
解答 解:已知抛物线y2=ax(a>0)与直线x=1围成的封闭图形的面积为$\frac{4}{3}$,
利用定积分,面积S=∫01[$\sqrt{ax}$-(-$\sqrt{ax}$)]dx=∫012$\sqrt{ax}$dx=$\frac{4}{3}$$\sqrt{a}$=$\frac{4}{3}$,得a=1,
利用二项式定理求系数的方法,Tr+1=C20r•x20-2r,
依题意令20-2r=-16,得r=18,即二项式展开式中含x-16项的系数为C2018=190.
故答案为190.
点评 本题考查定积分在求面积中的应用及利用二项式定理求二项式系数的试题.

练习册系列答案
相关题目
13. 某小卖部为了研究气温对热饮销售的影响,经过统计,得到一个卖出的热饮杯数y与当天气温(平均温度)x/°C的对比表:
某小卖部为了研究气温对热饮销售的影响,经过统计,得到一个卖出的热饮杯数y与当天气温(平均温度)x/°C的对比表:
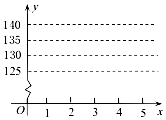
(1)请在图a中画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$;
(3)如果某天的气温是5°C,试根据(2)求出的线性回归方程预测这天大约可以卖出的热饮杯数.
参考公式:最小二乘法求线性回归方程系数公式:$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-,{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.
参考数据:0×140+1×136+3×129+4×125=1023,(140+136+129+125)÷4=132.5.
 某小卖部为了研究气温对热饮销售的影响,经过统计,得到一个卖出的热饮杯数y与当天气温(平均温度)x/°C的对比表:
某小卖部为了研究气温对热饮销售的影响,经过统计,得到一个卖出的热饮杯数y与当天气温(平均温度)x/°C的对比表:| x | 0 | 1 | 3 | 4 |
| y | 140 | 136 | 129 | 125 |
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$;
(3)如果某天的气温是5°C,试根据(2)求出的线性回归方程预测这天大约可以卖出的热饮杯数.
参考公式:最小二乘法求线性回归方程系数公式:$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-,{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.
参考数据:0×140+1×136+3×129+4×125=1023,(140+136+129+125)÷4=132.5.
18.某校共有学生3000名,各年级男、女生人数如表所示,已知高一、高二年级共有男生1120人,现用分层抽样的方法在全校抽取60名学生,则应在高三年级抽取的学生人数为( )
| 高一年级 | 高二年级 | 高三年级 | |
| 女生 | 456 | 424 | y |
| 男生 | 644 | x | z |
| A. | 16 | B. | 18 | C. | 20 | D. | 24 |
8.命题“?x>0,x2+x>0”的否定是( )
| A. | ?x>0,x2+x≤0 | B. | ?x≤0,x2+x>0 | C. | ?x0>0,x02+x0≤0 | D. | ?x0≤0,x02+x0>0 |
12.下列有关命题的说法中,正确的是( )
| A. | 命题“若x2>1,则x>1”的否命题为“若x2>1,则x≤1” | |
| B. | 命题“若α>β,则sinα>sinβ”的逆否命题为真命题 | |
| C. | 命题“?x∈R,使得x2+x+1<0”的否定是“?x∈R,都有x2+x+1>0” | |
| D. | “x>1”是“x2+x-2>0”的充分不必要条件 |