题目内容
17.口袋中装有4个形状大小完全相同的小球,小球的编号分别为1,2,3,4,甲、乙依次有放回地随机抽取1个小球,取到小球的编号分别为a,b.在一次抽取中,若有两人抽取的编号相同,则称这两人为“好朋友”,则甲、乙两人成为“好朋友”的概率为$\frac{1}{4}$.分析 由题意知两人取球包含的基本事件总数n=16,其中满足两人为“好朋友”的共有4种情况,由此能求出甲、乙两人成为“好朋友”的概率.
解答 解:由题意知两人取球包含的基本事件总数n=16,分别为:
(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),
(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4),
其中满足两人为“好朋友”的共有4种情况,分别为:(1,1),(2,2),(3,3),(4,4),
∴甲、乙两人成为“好朋友”的概率为p=$\frac{4}{16}=\frac{1}{4}$.
故答案为:$\frac{1}{4}$.
点评 本题考查概率的求法,考查古典概型等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是基础题.

练习册系列答案
相关题目
7.已知集合M={x|x≥0},N={x|x2<1},则M∩N=( )
| A. | [0,1] | B. | [0,1) | C. | (0,1] | D. | (0,1) |
8.若a+i=(b+i)(2-i)(其中a,b是实数,i为虚数单位),则复数a+bi在复平面内所对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
5.已知集合M={0,1},集合N满足M∪N={0,1},则集合N共有( )个.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
12.有两个不透明的箱子,每个箱子都装有4个完全相同的小球,球上分别标有数字1、2、3、4,甲从其中一个箱子中摸出一个球,乙从另一个箱子摸出一个球,谁摸出的球上标的数字大谁就获胜(若数字相同则为平局),则甲获胜的概率为( )
| A. | $\frac{4}{9}$ | B. | $\frac{3}{4}$ | C. | $\frac{5}{8}$ | D. | $\frac{3}{8}$ |
6.定积分${∫}_{1}^{e}$$\frac{1}{x}$dx的值等于( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
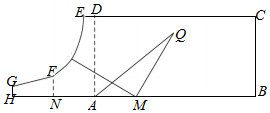 如图,某地区有一块长方形植物园ABCD,AB=8(百米),BC=4(百米),植物园西侧有一块荒地,现计划利用该荒地扩大植物园面积,使得新的植物园为HBCEFG满足下列要求:E在CD的延长线上,H在BA的延长线上,DE=0.5(百米),AH=4(百米),N为AH的中点,FN⊥AH,EF为曲线段,它上面的任意一点到AD与AH的距离乘积为定值,FG,GH均为线段,GH⊥HA,GH=0.5(百米).
如图,某地区有一块长方形植物园ABCD,AB=8(百米),BC=4(百米),植物园西侧有一块荒地,现计划利用该荒地扩大植物园面积,使得新的植物园为HBCEFG满足下列要求:E在CD的延长线上,H在BA的延长线上,DE=0.5(百米),AH=4(百米),N为AH的中点,FN⊥AH,EF为曲线段,它上面的任意一点到AD与AH的距离乘积为定值,FG,GH均为线段,GH⊥HA,GH=0.5(百米).